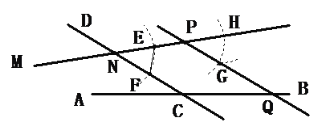
【题目】读句画图并完成计算:如图,直线AB与直线CD交于点C ,

(1)过点P作PQ∥CD,交AB于点Q;
(2)过P作PR⊥CD于点R;
(3)若∠DCB=150,求∠PQC的度数.
参考答案:
【答案】(1)详见解析;(2)详见解析;(3)30°.
【解析】
(1)根据“过一点做已知直线的平行线”的方法作图即可.
(2)根据“过一点做已知直线的垂线”的方法作图即可.
(3)根据两直线平行,同旁内角互补这一性质解决即可.
(1)作法:
1、过P作直线PM交CD于N,
2,以N为圆心适当长为半径画弧,交MP于E,交CD于F,
3、以P为圆心,同样长为半径画弧,交MP于H,
4、以H为圆心,EF长为半径画弧,交前弧于G,
则直线PG为所求.
(2)以点P为圆心,以一定长度为半径,作弧,交 CD于J、K两点,分别以
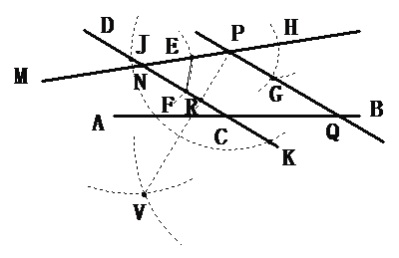
J、K为圆心以以大于![]() JK长为半径作弧,交与点V,连接PV,交CD与点R,连接PR,PR即为所求的垂线.
JK长为半径作弧,交与点V,连接PV,交CD与点R,连接PR,PR即为所求的垂线.
(3)∵ PQ∥CD, ∠DCB=150
∴∠PQC的度数为180°-50°=30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富课外活动,某校将购买一些乒乓球拍和乒乓球,某商场销售一种乒乓球拍和乒乓球,乒乓球拍每副定价80元,乒乓球每盒定价20元,“国庆节”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一副乒乓球拍送一盒乒乓球;
方案二:乒乓球拍和乒乓球都按定价的90%付款.
某校要到该商场购买乒乓球拍20副,乒乓球
 盒(
盒( >20且为整数).
>20且为整数).(1)若按方案一购买,需付款 元(用含
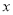 的整式表示,要化简); 若按方案二购买,需付款 元(用含
的整式表示,要化简); 若按方案二购买,需付款 元(用含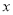 的整式表示,要化简).
的整式表示,要化简).(2)若
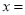 30,通过计算说明此时按哪种方案购买较为合算?
30,通过计算说明此时按哪种方案购买较为合算?(3)当
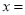 30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=6,AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为( )
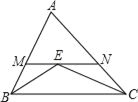
A. 12B. 10C. 8D. 不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,∠A=30°,在同一平面内,以对角线BD为底边作顶角为120°的等腰三角形BDE,则∠EBC的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在等边△ABC中取点P,使得PA,PB,PC的长分别为3,4,5,将线段AP以点A为旋转中心顺时针旋转60°得到线段AD,连接BD,下列结论:
①△ABD可以由△APC绕点A顺时针旋转60°得到;②点P与点D的距离为3;③∠APB=150°;
④S△APC+S△APB=
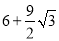 ,其中正确的结论有( )
,其中正确的结论有( )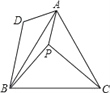
A. ①②④B. ①③④C. ①②③D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=k1x+2与反比例函数y2=
 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.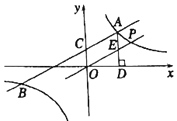
(1)k1= ,k2= ;
(2)根据函数图象可知,当y1>y2时,x的取值范围是 ;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求直线OP的解析式.
-
科目: 来源: 题型:
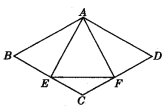
查看答案和解析>>【题目】已知:如图所示,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
(1)试说明:AE=AF;
(2)若∠B=60°,点E,F分别为BC和CD的中点,试说明:△AEF为等边三角形.
相关试题

