【题目】如图,一次函数y1=k1x+2与反比例函数y2=![]() 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
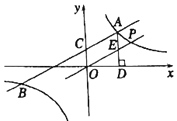
(1)k1= ,k2= ;
(2)根据函数图象可知,当y1>y2时,x的取值范围是 ;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求直线OP的解析式.
参考答案:
【答案】(1)![]() ,16;(2)﹣8<x<0或x>4;(3)y=
,16;(2)﹣8<x<0或x>4;(3)y=![]() .
.
【解析】
(1)先把![]() 点坐标代入入
点坐标代入入![]() 可确定一次函数解析式,再把
可确定一次函数解析式,再把![]() 代入
代入![]() 可确定反比例函数解析式;
可确定反比例函数解析式;
(2)观察函数图象得到当![]() 或
或![]() ,一次函数图象都在反比例函数图象上方;
,一次函数图象都在反比例函数图象上方;
(3)先确定点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,再计算出
,再计算出![]() ,由
,由![]() 可求得
可求得![]() ,可求得
,可求得![]() ,则可求得
,则可求得![]() 的坐标为,然后确定直线
的坐标为,然后确定直线![]() 的解析式.
的解析式.
解:(1)把![]() 代入
代入![]() 得
得![]() ,解得
,解得![]() ,
,
![]() 一次函数解析式为
一次函数解析式为![]() ;
;
把![]() 代入
代入![]() 得
得![]() ,
,
![]() 反比例函数解析式为
反比例函数解析式为![]() ,
,
故答案为:![]() ,16;
,16;
(2)![]() 当
当![]() 时即直线在反比例函数图象的上方时对应的
时即直线在反比例函数图象的上方时对应的![]() 的取值范围,
的取值范围,
![]() 或
或![]() ;
;
故答案为:![]() 或
或![]() ;
;
(3)把![]() 代入
代入![]() 得
得![]() ,解得
,解得![]() ,
,
![]() 点
点![]() 的坐标是
的坐标是![]() ,而点
,而点![]() 的坐标是
的坐标是![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,把
,把![]() 代入得
代入得![]() ,解得
,解得![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,∠A=30°,在同一平面内,以对角线BD为底边作顶角为120°的等腰三角形BDE,则∠EBC的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】读句画图并完成计算:如图,直线AB与直线CD交于点C ,

(1)过点P作PQ∥CD,交AB于点Q;
(2)过P作PR⊥CD于点R;
(3)若∠DCB=150,求∠PQC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在等边△ABC中取点P,使得PA,PB,PC的长分别为3,4,5,将线段AP以点A为旋转中心顺时针旋转60°得到线段AD,连接BD,下列结论:
①△ABD可以由△APC绕点A顺时针旋转60°得到;②点P与点D的距离为3;③∠APB=150°;
④S△APC+S△APB=
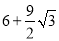 ,其中正确的结论有( )
,其中正确的结论有( )
A. ①②④B. ①③④C. ①②③D. ②③④
-
科目: 来源: 题型:
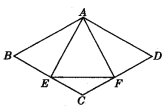
查看答案和解析>>【题目】已知:如图所示,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
(1)试说明:AE=AF;
(2)若∠B=60°,点E,F分别为BC和CD的中点,试说明:△AEF为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,
 点P从点A出发,沿折线AB-BC向终点C运动,在AB上以每秒8个单位长度的速度运动,在BC上以每秒2个单位长度的速度运动.动点Q从点C出发,沿CA方向以每秒
点P从点A出发,沿折线AB-BC向终点C运动,在AB上以每秒8个单位长度的速度运动,在BC上以每秒2个单位长度的速度运动.动点Q从点C出发,沿CA方向以每秒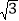 个单位长度的速度运动.P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P的运动时间为t秒.
个单位长度的速度运动.P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P的运动时间为t秒.(1)用含t的代数式表示线段AQ的长.
(2)当点P在线段AB上运动时,求PQ与△ABC一边垂直时t的值.
(3)设△APQ的面积为S(S>0),求S与t的函数关系式.
(4)当△APQ是以PQ为腰的等腰三角形时,直接写出t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.
利用数形结合思想回答下列问题:
(1)数轴上表示1和3两点之间的距离 .数轴上表示-12和-6的两点之间的距离是 .
(2)数轴上表示x和-4的两点之间的距离表示为 .
(3)|x-2|+|x+4|的最小值为 时,能使|x-2|+|x+4|取最小值的所有整数x的和是 .
(4)若数轴上两点A、B对应的数分别是-1、3,现在点A、点B分别以2个单位长度/秒和0.5个单位长度/秒的速度同时向右运动,当点A与点B之间的距离为3个单位长度时,求点A所对应的数是多少?

相关试题

