【题目】已知,抛物线y=ax+bx+4与x轴交于点A(-3,0)和B(2,0),与y轴交于点C.
(1)求抛物线的解析式;
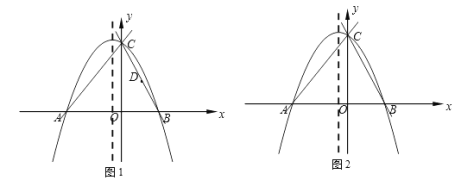
(2)如图1,若点D为CB的中点,将线段DB绕点D旋转,点B的对应点为点G,当点G恰好落在抛物线的对称轴上时,求点G的坐标;
(3)如图2,若点D为直线BC或直线AC上的一点,E为x轴上一动点,抛物线y=ax+bx+4对称轴上是否存在点F,使以B,D,F,E为顶点的四边形为菱形?若存在,请求出点F的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)抛物线的解析式为![]() ;
;
(2)点G的坐标![]() 或
或![]()
(3)点F的坐标为![]() ,
, ![]() ,
,![]() ,
,![]()
【解析】
试题(1)将A(-3,0)和B(2,0)两点代入解析式,求出a、b的值,即可求得抛物线的解析式;(2))设点G的坐标为![]() ,过点D作DH⊥对称轴于点H,因点D是BC的中点,可得点D的坐标为
,过点D作DH⊥对称轴于点H,因点D是BC的中点,可得点D的坐标为![]() ,
,![]() ,由折叠的性质可得DH=DB,根据勾股定理可得
,由折叠的性质可得DH=DB,根据勾股定理可得![]() ,解得y的值,即可得点G的坐标;(3)分当BE为对角线和BE为菱形的边时两种情况讨论求解即可.
,解得y的值,即可得点G的坐标;(3)分当BE为对角线和BE为菱形的边时两种情况讨论求解即可.
试题解析:
(1)由题意得![]() ,
,
解得,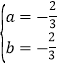
∴![]()
(2)设点G的坐标为![]()
过点D作DH⊥对称轴于点H
∵点D是BC的中点
∴点D的坐标为![]() ,
,![]()
由折叠得,DH=DB
∴![]()
∴![]()
∴点G的坐标为![]() 或
或![]()
(3)①当BE为对角线时,因为菱形的对角线互相垂直平分,所以此时D即为对称轴与AC的交点,F为点D关于x轴的对称点
设![]()
∵C![]() ,A
,A![]()
∴![]()
∴![]()
∴![]()
∴当![]() 时,
时,![]()
∴D![]()
∴F![]()
②当BE为菱形的边时,有DF∥BE
I)当点D在直线BC上时
易得![]()
设D![]() ,则点F
,则点F![]()
∵四边形BDFE是菱形
∴FD=DB
根据勾股定理得, ![]()
解得:![]() ,
,![]()
∴F![]() 或
或![]()
II)当点D在直线AC上时
设D![]() ,则点F
,则点F![]()
∵四边形BFDE是菱形
∴FD=FB
根据勾股定理得, ![]()
解得:![]() (舍去),
(舍去),![]()
∴F![]()
综上所述,点F的坐标分别为:![]() ,
, ![]() ,
,
![]() ,
,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
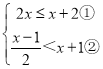
请结合题意填空,完成本题解答:
(1)解不等式①,得______;
(2)解不等式②,得______;
(3)把不等式①和②的解集在数轴上表示出来;
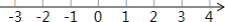
(4)原不等式组的解集为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知BD是△ABC的角平分线,ED⊥BC,∠BAC=90°,∠C=30°.

(1)求证:CE=BE;
(2)若AD=3,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某产品每件成本28元,在试销阶段产品的日销售量y(件)与每件产品的日销售价x(元)之间的关系如图中的折线所示.为维持市场物价平衡,最高售价不得高出83元.
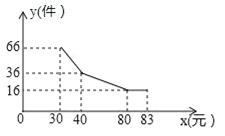
(1)求y与x之间的函数关系式;
(2)要使每日的销售利润w最大,每件产品的日销售价应定为多少元?此时每日销售利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角标系中,△ABC的三个顶点坐标为A(-3,1)、B(-4,-3)、C(-2,-4),△ABC绕原点顺时针旋转180°,得到△A1B1C1再将△A1B1C1向左平移5个单位得到△A2B2C2.
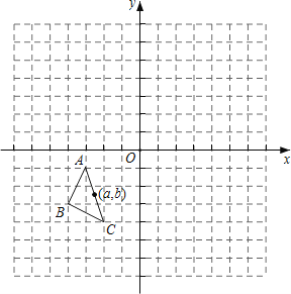
(1)画出△A1B1C1,并写出点A的对应点A1的坐标;
(2)画出△A2B2C2,并写出点A的对应点A2的坐标;
(3)P(a,b)是△ABC的边AC上一点,△ABC经旋转,平移后点P的对应点分别为P1、P2,请直接写出点P2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:等腰三角形两腰上的高相等.

(1)请你写出它的逆命题:______.
(2)逆命题是真命题吗?若是,请证明;若不是,请举出反例(要求:画出图形,写出已知,求证和证明过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
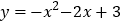 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=
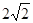 DQ,求点F的坐标.
DQ,求点F的坐标.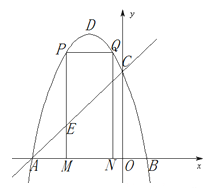
相关试题

