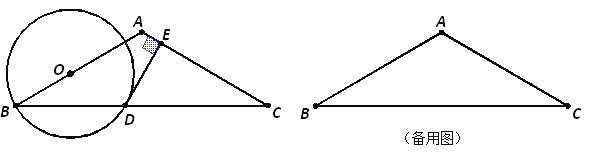
【题目】如图,在△ABC中,AB=AC=10,∠B=30°,O是线段AB上的一个动点,以O为圆心,OB为半径作⊙O交BC于点D,过点D作直线AC的垂线,垂足为E.
(1)求证:DE是⊙O的切线;
(2)设OB=x,求∠ODE的内部与△ABC重合部分的面积y的最大值.
参考答案:
【答案】(1)证明见解析;
(2)①当x=![]() 时,S△ODF最大,最大值为
时,S△ODF最大,最大值为![]() ;②当x=6时,重合部分的面积最大,最大值为10
;②当x=6时,重合部分的面积最大,最大值为10![]() .
.
【解析】试题分析:(1)由等腰三角形的性质可得∠C=∠B,∠ODB=∠C,从而∠ODB=∠C,根据同位角相等两直线平行可证OD∥AC,进而可证明结论;(2)①当点E在CA的延长线上时,设DE与AB交于点F,围成的图形为△ODF; ②当点E在线段AC上时,围成的图形为梯形AODE.根据三角形和梯形的面积公式列出函数关系式,利用二次函数的性质求解.
证明:(1)连接OD,
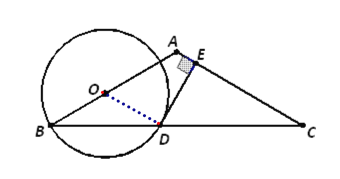
∵AB=AC,
∴∠C=∠B.
∵OB=OD,
∴∠ODB=∠B
∴∠ODB=∠C
∴OD∥AC.
∵DE⊥AC,
∴OD⊥DE,
∴DE是⊙O的切线.
(2)①当点E在CA的延长线上时,设DE与AB交于点F,围成的图形为△ODF.
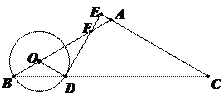
∵OD= OB= x,∠B=30°,∴∠FOD=60°,
∵∠ODE=90°,∴DF=![]() x,
x,
∴S△ODF=![]() x·
x·![]() x=
x= ![]() x
x![]() ,(0<x≤
,(0<x≤![]() )
)
当x=![]() 时,S△ODF最大,最大值为
时,S△ODF最大,最大值为![]()
![]() ;
;
②当点E在线段AC上时,围成的图形为梯形AODE.

∵AB=AC=10,∠B=30°,∴BC=10![]() ,
,
作OH⊥BC,∵OD= OB= x,∠B=30°,
∴BD= 2BH=![]() x,∴CD= 10
x,∴CD= 10![]()
![]() x,
x,
∵∠C=30°,∠DEC=90°,
∴DE=![]() (10
(10![]() -
-![]() x),CE=
x),CE=![]() (10
(10![]() -
-![]() x)=15-
x)=15-![]() x,∴AE=
x,∴AE=![]() x-5,
x-5,
∴S梯形AODE= ![]() (
(![]() x-5+ x)·
x-5+ x)·![]() (10
(10![]() -
-![]() x)=
x)= ![]() (-x
(-x![]() +12 x-20) (
+12 x-20) (![]() <x<10)
<x<10)
当x=6时,S梯形AODE最大,最大值为10![]() ;
;
综上所述,当x=6时,重合部分的面积最大,最大值为10![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提倡节约用水,我县自来水公司每月只给某单位计划内用水200吨,计划内用水每吨收费2.4元,超计划部分每吨按3.6元收费.
⑴用代数式表示下列问题(最后结果需化简 ):设用水量为
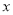 吨,当用水量小于等于200吨时,需付款多少元?当用水量大于200吨时,需付款多少元?
吨,当用水量小于等于200吨时,需付款多少元?当用水量大于200吨时,需付款多少元?⑵若某单位4月份缴纳水费840元,则该单位用水量多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(14分)小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员A:月销售件数200件,月总收入2400元;
营业员B:月销售件数300件,月总收入2700元;
假设营业员的月基本工资为
 元,销售每件服装奖励
元,销售每件服装奖励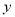 元.
元.(1)求
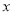 、
、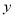 的值;
的值;(2)若某营业员的月总收入不低于3100元,那么他当月至少要卖服装多少件?
(3)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲3件,乙2件,丙1件共需350元;如果购买甲1件,乙2件,丙3件共需370元.某顾客想购买甲、乙、丙各一件共需多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
定义:有三个内角相等的四边形叫“和谐四边形”.
(1)在“和谐四边形”
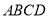 中,若
中,若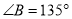 ,则
,则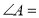 ;
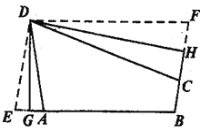
;(2)如图,折叠平行四边形纸片
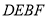 ,使顶点
,使顶点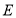 ,
,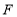 分别落在边
分别落在边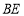 ,
,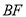 上的点
上的点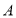 ,
,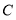 处,折痕分别为
处,折痕分别为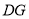 ,
,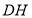 .
.求证:四边形
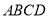 是“和谐四边形”.
是“和谐四边形”. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)中的x与y的部分对应值如下表所示,则下列结论中,正确的个数有( )
x
-7
-6
-5
-4
-3
-2
y
-27
-13
-3
3
5
3
①当x<-4时,y<3②当x=1时,y的值为-13;③-2是方程ax2+(b-2)x+c-7=0的一个根;④方程ax2+bx+c=6有两个不相等的实数根.
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
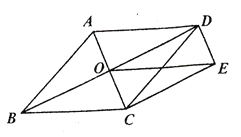
查看答案和解析>>【题目】如图,菱形
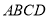 的对角线
的对角线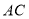 、
、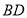 相交于点
相交于点 ,
,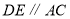 ,
,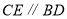 ,连接
,连接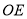 .
.
(1)求证:
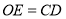 ;
;(2)探究:当
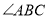 等于多少度时,四边形
等于多少度时,四边形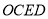 是正方形?并证明你的结论.
是正方形?并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是双曲线y=
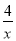 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
相关试题

