【题目】如图,菱形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,连接
,连接![]() .
.
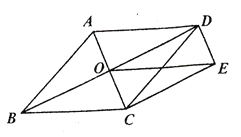
(1)求证:![]() ;
;
(2)探究:当![]() 等于多少度时,四边形
等于多少度时,四边形![]() 是正方形?并证明你的结论.
是正方形?并证明你的结论.
参考答案:
【答案】(1)见解析;(2)当![]() 时,四边形OCED为正方形,见解析.
时,四边形OCED为正方形,见解析.
【解析】
(1)先求出四边形OCED是平行四边形,再根据菱形的对角线互相垂直求出∠COD=90°,证明OCED是矩形,由矩形的性质可得OE=DC;
(2)当∠ABC=90°时,四边形OCED是正方形,根据正方形的判定方法证明即可.
解:(1)证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∵四边形ABCD是菱形,
∴∠COD=90°,
∴四边形OCED是矩形,
∴OE=DC;
(2)当∠ABC=90°时,四边形OCED是正方形,
理由如下:
∵四边形ABCD是菱形,∠ABC=90°,
∴四边形ABCD是正方形,
∴DO=CO,
又∵四边形OCED是矩形,
∴四边形OCED是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
定义:有三个内角相等的四边形叫“和谐四边形”.
(1)在“和谐四边形”
 中,若
中,若 ,则
,则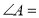 ;
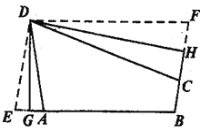
;(2)如图,折叠平行四边形纸片
 ,使顶点
,使顶点 ,
, 分别落在边
分别落在边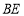 ,
,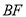 上的点
上的点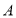 ,
,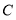 处,折痕分别为
处,折痕分别为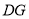 ,
,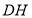 .
.求证:四边形
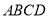 是“和谐四边形”.
是“和谐四边形”. -
科目: 来源: 题型:
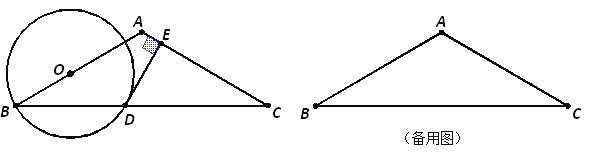
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=10,∠B=30°,O是线段AB上的一个动点,以O为圆心,OB为半径作⊙O交BC于点D,过点D作直线AC的垂线,垂足为E.
(1)求证:DE是⊙O的切线;
(2)设OB=x,求∠ODE的内部与△ABC重合部分的面积y的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)中的x与y的部分对应值如下表所示,则下列结论中,正确的个数有( )
x
-7
-6
-5
-4
-3
-2
y
-27
-13
-3
3
5
3
①当x<-4时,y<3②当x=1时,y的值为-13;③-2是方程ax2+(b-2)x+c-7=0的一个根;④方程ax2+bx+c=6有两个不相等的实数根.
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是双曲线y=
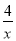 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】学生刘明,对某校六1班上学期期末的数学成绩(成绩取整数,满分为100分)作了统计,发现这个班每个人的成绩各不相同,并据此绘制成如下频数分布表和频数分布直方图.请你根据图表提供的信息,解答下列问题:
分组
49.5~59.5
59.5~69.5
69.5~79.5
79.5~89.5
89.5~100.5
合计
频数
2
8
20
a
4
c
频率
0.04
b
0.40
0.32
0.08
1
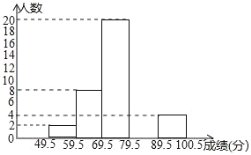
(1)频数、频率分布表中a=____,b=_____,c=_____;
(2)补全频数分布直方图;
(3)如果要画该班上学期期末数学成绩的扇形统计图,那么分数在69.5﹣79.5之间的扇形圆心角的度数是_______.
(4)张亮同学成绩为79分,他说:“我们班上比我成绩高的人还有
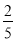 ,我要继续努力.”他的说法正确吗?请说明理由.
,我要继续努力.”他的说法正确吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】P是三角形
 内一点,射线PD//AC ,射线PB//AB .
内一点,射线PD//AC ,射线PB//AB .(1)当点D,E分别在AB,BC 上时,
①补全图1:
②猜想
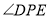 与
与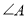 的数量关系,并证明;,
的数量关系,并证明;,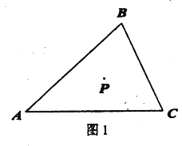
(2)当点
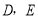 都在线段
都在线段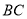 上时,请先画出图形,想一想你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由
上时,请先画出图形,想一想你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由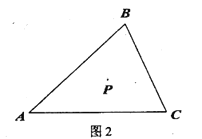
相关试题

