【题目】为提倡节约用水,我县自来水公司每月只给某单位计划内用水200吨,计划内用水每吨收费2.4元,超计划部分每吨按3.6元收费.
⑴用代数式表示下列问题(最后结果需化简 ):设用水量为![]() 吨,当用水量小于等于200吨时,需付款多少元?当用水量大于200吨时,需付款多少元?
吨,当用水量小于等于200吨时,需付款多少元?当用水量大于200吨时,需付款多少元?
⑵若某单位4月份缴纳水费840元,则该单位用水量多少吨?
参考答案:
【答案】⑴当用水量小于等于200吨,需付款![]() ,当用水量大于200吨,需付款
,当用水量大于200吨,需付款![]() 元;⑵该单位用水量300吨.
元;⑵该单位用水量300吨.
【解析】
(1)根据计划内用水每吨收费2.4元,可求出用水量小于等于200吨时,需付款的钱数;再根据超计划部分每吨按3.6元收费,可求出用水量大于200吨时,需付款钱数;
(2)先判断该单位4月份用水量是否超过200吨,再根据(1)中得出的关系式列方程求解即可.
解:(1)由题意可知:当用水量小于等于200吨,需付款![]()
当用水量大于200吨,需付款![]() 元
元
(2)因为![]()
所以该单位4月份用水量超过200吨
根据题意得:![]()
解得:![]()
答:该单位用水量300吨.
-
科目: 来源: 题型:
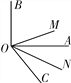
查看答案和解析>>【题目】如图,∠AOB为直角,∠AOC为锐角,且OM平分∠BOC,ON平分∠AOC.
(1)如果∠AOC=50°,求∠MON的度数;
(2)如果∠AOC为任意一个锐角,你能求出∠MON的度数吗?若能,请求出来,若不能,说明为什么?
-
科目: 来源: 题型:
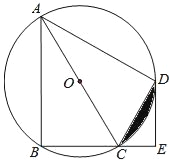
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,
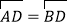 ,AC为直径,DE⊥BC,垂足为E.
,AC为直径,DE⊥BC,垂足为E.(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于实数a,b,我们可以用min{a,b}表示a,b两数中较小的数,例如min{3,-1}=-1,min{2,2}=2. 类似地,若函数y1、y2都是x的函数,则y=min{y1, y2}表示函数y1和y2的“取小函数”.
(1)设y1=x,y2=
 ,则函数y=min{x,
,则函数y=min{x,  }的图像应该是 中的实线部分.
}的图像应该是 中的实线部分.
(2)请在下图中用粗实线描出函数y=min{(x-2)2, (x+2)2}的图像,并写出该图像的三条不同性质:

① ;
② ;
③ ;
(3)函数y=min{(x-4)2, (x+2)2}的图像关于 对称.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(14分)小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员A:月销售件数200件,月总收入2400元;
营业员B:月销售件数300件,月总收入2700元;
假设营业员的月基本工资为
 元,销售每件服装奖励
元,销售每件服装奖励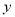 元.
元.(1)求
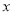 、
、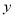 的值;
的值;(2)若某营业员的月总收入不低于3100元,那么他当月至少要卖服装多少件?
(3)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲3件,乙2件,丙1件共需350元;如果购买甲1件,乙2件,丙3件共需370元.某顾客想购买甲、乙、丙各一件共需多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
定义:有三个内角相等的四边形叫“和谐四边形”.
(1)在“和谐四边形”
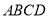 中,若
中,若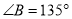 ,则
,则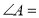 ;
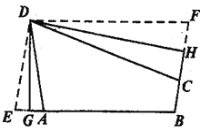
;(2)如图,折叠平行四边形纸片
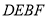 ,使顶点
,使顶点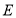 ,
,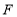 分别落在边
分别落在边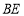 ,
,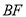 上的点
上的点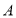 ,
,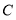 处,折痕分别为
处,折痕分别为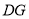 ,
,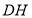 .
.求证:四边形
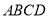 是“和谐四边形”.
是“和谐四边形”. -
科目: 来源: 题型:
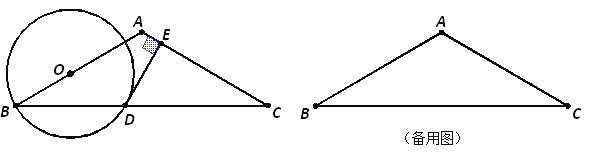
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=10,∠B=30°,O是线段AB上的一个动点,以O为圆心,OB为半径作⊙O交BC于点D,过点D作直线AC的垂线,垂足为E.
(1)求证:DE是⊙O的切线;
(2)设OB=x,求∠ODE的内部与△ABC重合部分的面积y的最大值.
相关试题

