【题目】如图,在平面直角坐标系中,把二元一次方程![]() 的若干个解用点表示出来,发现它们都落在同一条直线上.一般地,任何一个二元一次方程的所有解用点表示出来,它的图象就是一条直线.根据这个结论,解决下列问题:
的若干个解用点表示出来,发现它们都落在同一条直线上.一般地,任何一个二元一次方程的所有解用点表示出来,它的图象就是一条直线.根据这个结论,解决下列问题:
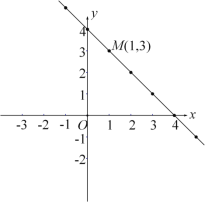
(1)根据图象判断二元一次方程![]() 的正整数解为 ;(写出所有正整数解)
的正整数解为 ;(写出所有正整数解)
(2)若在直线上取一点![]() (
(![]() ,
,![]() ),先向下平移
),先向下平移![]() 个单位长度,再向右平移
个单位长度,再向右平移![]() 个单位长度得到点M′,发现点M′又重新落在二元一次方程
个单位长度得到点M′,发现点M′又重新落在二元一次方程![]() 的图象上,试探究
的图象上,试探究![]() ,
,![]() 之间满足的数量关系.
之间满足的数量关系.
参考答案:
【答案】(1)(1)![]() ,
,![]() ,
,![]() (2)a=b
(2)a=b
【解析】
(1)根据函数图象结合函数即可解答.
(2)根据平移的性质求出M的坐标,再把M的坐标代入解析式即可解答.
解:(1)![]() ,
,![]() ,
,![]()
(2)点M移动后的坐标为(1+b,3![]() a)
a)
∵(1+b,3![]() a)在
a)在![]() 上
上
∴ 1+b+3![]() a=4
a=4
解得 a=b
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注.某单位计划在室内安装空气净化装置,需购进A、B两种设备.每台B种设备价格比每台A种设备价格多0.7万元,花3万元购买A种设备和花7.2万元购买B种设备的数量相同.
(1)求A种、B种设备每台各多少万元?
(2)根据单位实际情况,需购进A、B两种设备共20台,总费用不高于15万元,求A种设备至少要购买多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一座桥如图,桥下水面宽度AB是20米,高CD是4米.要使高为3米的船通过,则其宽度须不超过多少米.
(1)如图1,若把桥看做是抛物线的一部分,建立如图坐标系.
①求抛物线的解析式;
②要使高为3米的船通过,则其宽度须不超过多少米?
(2)如图2,若把桥看做是圆的一部分.
①求圆的半径;
②要使高为3米的船通过,则其宽度须不超过多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个运输公司有甲、乙两种货车,两次满载的运输情况如下表:
甲种货车辆数
乙种货车辆数
合计运货吨数
第一次
2
4
18
第二次
5
6
35
(1)求甲、乙两种货车每次满载分别能运输多少吨货物;
(2)现有一批重34吨的货物需要运输,而甲、乙两种货车运输的保养费用分别为80元/辆和40元/辆.公司打算由甲、乙两种货车共10辆来完成这次运输,为了使保养费用不超过700元,公司该如何安排甲、乙两种货车来完成这次运输任务.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了迎接体育中考,3月底对初三某班学生进行了一次跳绳测试,测试成绩分别记为A,B,C,D,E共5个等级(其中D,E为优良),并绘制成了统计图1.在进行了为期一个月的特训后,4月底对同一批学生又进行了一次跳绳测试,发现A类的人数没有发生变化,并将成绩绘制成统计图2.请根据图中提供的信息,解答下列问题:
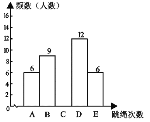

图1 图2
(1)求此次参加测试的学生人数;
(2)补全频数分布直方图和扇形统计图C为____;
(3)请估计该校九年级500名学生在进行一个月的特训后,优良人数增加了多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题的逆命题成立的是( ).
A.全等三角形的对应角相等
B.若三角形的三边满足
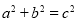 ,则该三角形是直角三角形
,则该三角形是直角三角形C.对顶角相等
D.同位角互补,两直线平行
相关试题

