【题目】近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注.某单位计划在室内安装空气净化装置,需购进A、B两种设备.每台B种设备价格比每台A种设备价格多0.7万元,花3万元购买A种设备和花7.2万元购买B种设备的数量相同.
(1)求A种、B种设备每台各多少万元?
(2)根据单位实际情况,需购进A、B两种设备共20台,总费用不高于15万元,求A种设备至少要购买多少台?
参考答案:
【答案】(1)每台A种设备0.5万元,每台B种设备1.2万元;(2)13.
【解析】
试题(1)设每台A种设备x万元,则每台B种设备(x+0.7)万元,根据数量=总价÷单价结合花3万元购买A种设备和花7.2万元购买B种设备的数量相同,即可得出关于x的分式方程,解之并检验后即可得出结论;
(2)设购买A种设备m台,则购买B种设备(20﹣m)台,根据总价=单价×数量结合总费用不高于15万元,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,取其内的最小正整数即可.
试题解析:(1)设每台A种设备x万元,则每台B种设备(x+0.7)万元,
根据题意得:![]() ,
,
解得:x=0.5.
经检验,x=0.5是原方程的解,
∴x+0.7=1.2.
答:每台A种设备0.5万元,每台B种设备1.2万元.
(2)设购买A种设备m台,则购买B种设备(20﹣m)台,
根据题意得:0.5m+1.2(20﹣m)≤15,
解得:m≥![]() .
.
∵m为整数,
∴m≥13.
答:A种设备至少要购买13台.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明:
如图,∠C=50°,E是BA延长线上的一点,过点A作
 //BC﹒若AD平分∠CAE,求∠B的度数.
//BC﹒若AD平分∠CAE,求∠B的度数.
解:∵
 //BC,∠C=50°( 已知 ),
//BC,∠C=50°( 已知 ),∴∠2= = °( ).
又∵AD平分∠CAE( 已知 ),
∴ =∠2=50°( ).
又∵
 //BC(已知),
//BC(已知),∴∠B= = °( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是计算机中的一种益智小游戏“扫雷”的画面,在一个9×9的小方格的正方形雷区中,随机埋藏着10颗地雷,每个小方格内最多只能埋藏1颗地雷。

小红在游戏开始时首先随机地点击一个方格,该方格中出现了数字“3”,其意义表示该格的外围区域(图中阴影部分,记为A区域)有3颗地雷;接着,小红又点击了左上角第一个方格,出现了数字“1”,其外围区域(图中阴影部分)记为B区域;“A区域与B区域以及出现数字‘1’和‘3’两格”以外的部分记为C区域。小红在下一步点击时要尽可能地避开地雷,那么她应点击A. B. C中的哪个区域?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一座桥如图,桥下水面宽度AB是20米,高CD是4米.要使高为3米的船通过,则其宽度须不超过多少米.
(1)如图1,若把桥看做是抛物线的一部分,建立如图坐标系.
①求抛物线的解析式;
②要使高为3米的船通过,则其宽度须不超过多少米?
(2)如图2,若把桥看做是圆的一部分.
①求圆的半径;
②要使高为3米的船通过,则其宽度须不超过多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,把二元一次方程
 的若干个解用点表示出来,发现它们都落在同一条直线上.一般地,任何一个二元一次方程的所有解用点表示出来,它的图象就是一条直线.根据这个结论,解决下列问题:
的若干个解用点表示出来,发现它们都落在同一条直线上.一般地,任何一个二元一次方程的所有解用点表示出来,它的图象就是一条直线.根据这个结论,解决下列问题: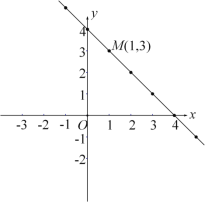
(1)根据图象判断二元一次方程
 的正整数解为 ;(写出所有正整数解)
的正整数解为 ;(写出所有正整数解)(2)若在直线上取一点
 (
( ,
, ),先向下平移
),先向下平移 个单位长度,再向右平移
个单位长度,再向右平移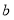 个单位长度得到点M′,发现点M′又重新落在二元一次方程
个单位长度得到点M′,发现点M′又重新落在二元一次方程 的图象上,试探究
的图象上,试探究 ,
,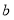 之间满足的数量关系.
之间满足的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个运输公司有甲、乙两种货车,两次满载的运输情况如下表:
甲种货车辆数
乙种货车辆数
合计运货吨数
第一次
2
4
18
第二次
5
6
35
(1)求甲、乙两种货车每次满载分别能运输多少吨货物;
(2)现有一批重34吨的货物需要运输,而甲、乙两种货车运输的保养费用分别为80元/辆和40元/辆.公司打算由甲、乙两种货车共10辆来完成这次运输,为了使保养费用不超过700元,公司该如何安排甲、乙两种货车来完成这次运输任务.
相关试题

