【题目】某校为了迎接体育中考,3月底对初三某班学生进行了一次跳绳测试,测试成绩分别记为A,B,C,D,E共5个等级(其中D,E为优良),并绘制成了统计图1.在进行了为期一个月的特训后,4月底对同一批学生又进行了一次跳绳测试,发现A类的人数没有发生变化,并将成绩绘制成统计图2.请根据图中提供的信息,解答下列问题:
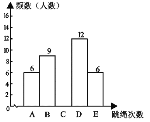

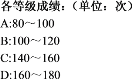
图1 图2
(1)求此次参加测试的学生人数;
(2)补全频数分布直方图和扇形统计图C为____;
(3)请估计该校九年级500名学生在进行一个月的特训后,优良人数增加了多少.
参考答案:
【答案】(1)40人 ;(2)见解析;17.5% ;(3)25人;
【解析】
(1)利用A得人数除以百分比占比即可解答.
(2)利用1-减去A,B,E,D的百分比,得到C的百分比,再利用总人数乘以C的百分比即可求出C的人数.
(3)求出D,E的百分比再乘以500即可解答.
解:(1)6÷15%=40(人)
(2)1-(15%+15%+17.5%+35%)=17.5%
40×0.175=7,
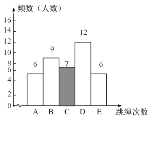
(3)(12+6)÷40= 45%
500×(50%-45%)=25(人)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一座桥如图,桥下水面宽度AB是20米,高CD是4米.要使高为3米的船通过,则其宽度须不超过多少米.
(1)如图1,若把桥看做是抛物线的一部分,建立如图坐标系.
①求抛物线的解析式;
②要使高为3米的船通过,则其宽度须不超过多少米?
(2)如图2,若把桥看做是圆的一部分.
①求圆的半径;
②要使高为3米的船通过,则其宽度须不超过多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,把二元一次方程
 的若干个解用点表示出来,发现它们都落在同一条直线上.一般地,任何一个二元一次方程的所有解用点表示出来,它的图象就是一条直线.根据这个结论,解决下列问题:
的若干个解用点表示出来,发现它们都落在同一条直线上.一般地,任何一个二元一次方程的所有解用点表示出来,它的图象就是一条直线.根据这个结论,解决下列问题: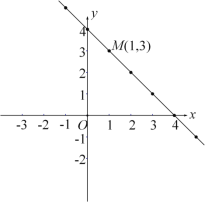
(1)根据图象判断二元一次方程
 的正整数解为 ;(写出所有正整数解)
的正整数解为 ;(写出所有正整数解)(2)若在直线上取一点
 (
( ,
, ),先向下平移
),先向下平移 个单位长度,再向右平移
个单位长度,再向右平移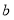 个单位长度得到点M′,发现点M′又重新落在二元一次方程
个单位长度得到点M′,发现点M′又重新落在二元一次方程 的图象上,试探究
的图象上,试探究 ,
,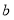 之间满足的数量关系.
之间满足的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个运输公司有甲、乙两种货车,两次满载的运输情况如下表:
甲种货车辆数
乙种货车辆数
合计运货吨数
第一次
2
4
18
第二次
5
6
35
(1)求甲、乙两种货车每次满载分别能运输多少吨货物;
(2)现有一批重34吨的货物需要运输,而甲、乙两种货车运输的保养费用分别为80元/辆和40元/辆.公司打算由甲、乙两种货车共10辆来完成这次运输,为了使保养费用不超过700元,公司该如何安排甲、乙两种货车来完成这次运输任务.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题的逆命题成立的是( ).
A.全等三角形的对应角相等
B.若三角形的三边满足
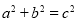 ,则该三角形是直角三角形
,则该三角形是直角三角形C.对顶角相等
D.同位角互补,两直线平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线
 ( a≠0)经过原点,顶点为A(h,k)(h≠0).
( a≠0)经过原点,顶点为A(h,k)(h≠0).(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线
 (t≠0)也经过A点,求a与t之间的关系式;
(t≠0)也经过A点,求a与t之间的关系式;(3)当点A在抛物线
 上,且-2≤h<1时,求a的取值范围.
上,且-2≤h<1时,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列判断错误的是( )

A. 如果∠2=∠4,那么AB∥CD B. 如果∠1=∠3,那么AB∥CD
C. 如果∠BAD+∠D=180°,那么AB∥CD D. 如果∠BAD+∠B=180,那么AD∥CD
相关试题

