【题目】如图所示,□ABCD的对角线AC,BD相交于点O,E、F、G、H分别是OA、OB、OC、OD的中点,那么□ABCD与四边形EFGH是否是位似图形?为什么?

参考答案:
【答案】是.
因为E,F,G,H分别是OA,OB,OC,OD的中点,所以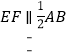 ,
,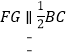 ,
,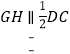 ,
,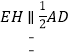 ,所以四边形EFGH是平行四边形,且□ABCD∽□EFGH.又各组对应点的连线相交于点O,所以□ABCD与四边形EFGH是位似图形,O为位似中心.
,所以四边形EFGH是平行四边形,且□ABCD∽□EFGH.又各组对应点的连线相交于点O,所以□ABCD与四边形EFGH是位似图形,O为位似中心.
【解析】
试题根据三角形中位线定理得到EF=HG,FE∥HG,根据平行四边形的判定定理证明四边形EFGH是平行四边形,再根据平行线的性质定理、相似多边形的判定定理证明.
解:是,
理由:∵E、F分别是OA、OB的中点,
∴FE=![]() AB,FE∥AB,
AB,FE∥AB,
G、H分别是OC、OD的中点,
∴HG=![]() CD,HG∥CD,
CD,HG∥CD,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴EF=HG,FE∥HG,
∴四边形EFGH是平行四边形;
∵FE∥AB,
∴∠OEF=∠OAB,
同理∠OEH=∠OAD,
∴∠HEF=∠DAB,
同理,∠EFG=∠ABC,∠FGH=∠BCD,∠GHE=∠CDA,![]() =
=![]() =
=![]() =
=![]() =
=![]() ,
,
∴平行四边形EFGH∽平行四边形ABCD,
又∵各组对边对应点得连线相交于点O,
∴平行四边形ABCD与四边形EFGH是位似图形,O为位似中心.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于点M,交DC于点N,设AE=x,BM=y,则y与x的大致图象是( )

A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,用棋子摆成的“上”字:

第一个“上”字 第二个“上”字 第三个“上”字
如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第四、第五个“上”字分别需用 和 枚棋子.
(2)第n个“上”字需用 枚棋子.
(3)如果某一图形共有102枚棋子,你知道它是第几个“上”字吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①点(-ab,c)在第四象限;②a+b+c<0;③
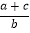 >1;④2a+b>0.其中正确的是_______(填序号).
>1;④2a+b>0.其中正确的是_______(填序号).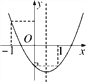
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B分别在反比例函数y=
 (x>0)、y=
(x>0)、y= (x>0)的图象上,且∠AOB=90°,∠B=30°,求y=
(x>0)的图象上,且∠AOB=90°,∠B=30°,求y= 的表达式.
的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
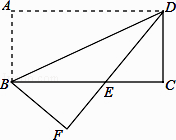
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在合肥大蜀山山顶有一斜坡AP的坡度为1∶2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座安徽卫视发射塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°,求:
(1)坡顶A到地面PQ的距离;
(2)发射塔BC的高度(结果保留为整数,参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01,tan14°≈0.25).


相关试题

