【题目】如图,在合肥大蜀山山顶有一斜坡AP的坡度为1∶2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座安徽卫视发射塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°,求:
(1)坡顶A到地面PQ的距离;
(2)发射塔BC的高度(结果保留为整数,参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01,tan14°≈0.25).

![]()
参考答案:
【答案】(1) 10米 (2) 19米
【解析】(1)过点A作AH⊥PQ,垂足为点H,利用斜坡AP的坡度为1:2.4,得出AH,PH,AH的关系求出即可;
(2)利用矩形性质求出设BC=x,则x+10=24+DH,再利用tan76°=![]() ,求出即可.
,求出即可.
(1)如图,过点A作AH⊥PQ,垂足为点H,
∵斜坡AP的坡度为1∶2.4,∴![]() ,
,
设AH=5k米,则PH=12k米,由勾股定理得AP=![]() =13k米,
=13k米,
∴13k=26,解得k=2,∴AH=10米,
答:坡顶A到地面PQ的距离为10米;
(2)如图,延长BC交PQ于点D,
∵BC⊥AC,AC∥PQ,∴BD⊥PQ,∴四边形AHDC是矩形,
∴CD=AH=10米,AC=DH,
∵∠BPD=45°,∴PD=BD.设BC=x米,由(1)可知PH=24米,
则x+10=24+DH,∴AC=DH=(x-14)米,
在Rt△ABC中,tan76°=![]() ,即
,即![]() ≈4.01,解得x≈19,
≈4.01,解得x≈19,
答:发射塔BC的高度约为19米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,□ABCD的对角线AC,BD相交于点O,E、F、G、H分别是OA、OB、OC、OD的中点,那么□ABCD与四边形EFGH是否是位似图形?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B分别在反比例函数y=
 (x>0)、y=
(x>0)、y= (x>0)的图象上,且∠AOB=90°,∠B=30°,求y=
(x>0)的图象上,且∠AOB=90°,∠B=30°,求y= 的表达式.
的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
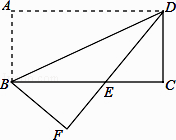
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,一次函数y=
 x+3的图像与y轴交于点A,点M在正比例函数y=
x+3的图像与y轴交于点A,点M在正比例函数y=  x的图像x>0的那部分上,且MO=MA(O为坐标原点).
x的图像x>0的那部分上,且MO=MA(O为坐标原点).
(1)求线段AM的长;
(2)若反比例函数y=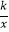 的图像经过点M关于y轴的对称点M′,求反比例函数解析式,并直接写出当x>0时,
的图像经过点M关于y轴的对称点M′,求反比例函数解析式,并直接写出当x>0时,  x+3与
x+3与 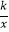 的大小关系.
的大小关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划投入一笔资金采购一批紧俏商品,经过市场调查发现,如果月初出售,可获利15﹪,并可用本金和利润再投资其他商品,到月末又可获利10﹪;如果月末出售可获利30﹪,但要付出仓储费用700元.
(1)若商场投资
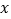 元,分别用含
元,分别用含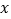 的代数式表示月初出售和月末出售所获得的利润;
的代数式表示月初出售和月末出售所获得的利润;(2)若商场投资40000元,问选择哪种销售方式获利较多?此时获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家超市以相同的价格出售同样的商品,但为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超过400元后,超过部分按原价七折优惠;在乙超市购买商品只按原价的八折优惠;设顾客累计购物
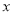 元(
元(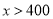 )
)(1)用含
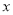 的代数式分别表示顾客在两家超市购买所付的费用。
的代数式分别表示顾客在两家超市购买所付的费用。(2)当
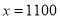 时,试比较顾客到哪家超市购物更加优惠。
时,试比较顾客到哪家超市购物更加优惠。
相关试题

