【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的.其中测得坡长AB=600米,BC=200米,坡角∠BAF=30°,∠CBE=45°.(结果保留根号)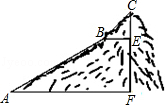
参考答案:
【答案】解:如图所示,过B作BG⊥AF于G,
则BG=EF、BE=GF,
∵AB=600,∠BAF=30°,
∴EF=BG= ![]() AB=300米,
AB=300米,
在Rt△BCE中,∵BC=200米,∠CBE=45°,
∴CE=BCsin∠CBE=200× ![]() =100
=100 ![]() (米),
(米),
∴CF=300+100 ![]() (米)
(米)
∴山峰的高度是(300+100 ![]() )米.
)米.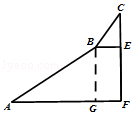
【解析】作BG⊥AF于G,在Rt△ABG中根据∠BAF=30°得出BG的长,从而得到EF的长,再在Rt△CBE中利用∠CBE的正弦计算出CE,然后计算CE和EF的和即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G、F,H为CG的中点,连接DE、EH、DH、FH.下列结论:①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若
 =
=  ,则3S△EDH=13S△DHC , 其中结论正确的有(填写序号).
,则3S△EDH=13S△DHC , 其中结论正确的有(填写序号). 
-
科目: 来源: 题型:
查看答案和解析>>【题目】提出命题:如图,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证:四边形ABCD是平行四边形.
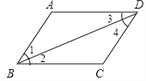
小明提供了如下解答过程:
证明:连接BD.
∵∠1+∠3=180-∠A,∠2+∠4=180―∠C,∠A=∠C,
∴ ∠1+∠3=∠2+∠4.
∵∠ABC=∠ADC,
∴∠1=∠4,∠2=∠3.
∴AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
反思交流:(1)请问小明的解法正确吗?如果有错,说明错在何处,并给出正确的证明过程.
(2)用语言叙述上述命题:___________________________________________________.
运用探究:(3)下列条件中,能确定四边形ABCD是平行四边形的是(_____)
A. ∠A∶∠B∶∠C∶∠D=1∶2∶3∶4 B. ∠A∶∠B∶∠C∶∠D=1∶3∶1∶3
C. ∠A∶∠B∶∠C∶∠D=2∶3∶3∶2 D. ∠A∶∠B∶∠C∶∠D=1∶1∶3∶3
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣64的立方根是( )
A.±8B.4C.﹣4D.16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平行四边形ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:BD与MN互相平分.
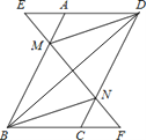
-
科目: 来源: 题型:
查看答案和解析>>【题目】第三届世界互联网大会(3rd World Internet Conference),是由中华人民共和国倡导并举办的互联网盛会,于2016年11月16日至18日在浙江乌镇举办.某初中学校为了了解本校学生对本次互联网大会的关注程度(关注程度分为:A.特别关注;B.一般关注;C.偶尔关注;D.不关注),随机抽取了部分学生进行调查,并将结果绘制成频数折线统计图1和扇形统计图2(不完整)请根据图中信息回答问题.
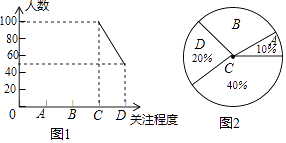
(1)此次抽样调查中,共调查了多少名学生?
(2)求出图2中扇形B所对的圆心角度数,并将图1补充完整.
(3)在这次调查中,九(1)班共有甲、乙、丙、丁四人“特别关注”本届互联网大会,现准备从四人中随机抽取两人进行交流,请用列表法或画树状图的方法求出抽取的两人恰好是甲和乙的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个底面直径为5 cm,高为18 cm的圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径为6cm,高为10cm的圆柱形玻璃中,能否完全装下?若装不下,那么瓶内水面还有多高?若未能装满,求杯内水面离杯口的距离.
相关试题

