【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=22,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)出数轴上点B表示的数 ;点P表示的数 (用含t的代数式表示)
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问多少秒时P、Q之间的距离恰好等于2?
(3)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?
(4)若M为AP的中点,N为BP的中点,在点P运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由,若不变,请你画出图形,并求出线段MN的长.
![]()
参考答案:
【答案】(1)﹣14,8﹣5t;(2)2.5或3秒时P、Q之间的距离恰好等于2;(3)点P运动11秒时追上点Q;(4)线段MN的长度不发生变化,其值为11,见解析.
【解析】
(1)根据已知可得B点表示的数为8﹣22;点P表示的数为8﹣5t;(2)设t秒时P、Q之间的距离恰好等于2.分①点P、Q相遇之前和②点P、Q相遇之后两种情况求t值即可;(3)设点P运动x秒时,在点C处追上点Q,则AC=5x,BC=3x,根据AC﹣BC=AB,列出方程求解即可;(3)分①当点P在点A、B两点之间运动时,②当点P运动到点B的左侧时,利用中点的定义和线段的和差求出MN的长即可.
(1)∵点A表示的数为8,B在A点左边,AB=22,
∴点B表示的数是8﹣22=﹣14,
∵动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,
∴点P表示的数是8﹣5t.
故答案为:﹣14,8﹣5t;
(2)若点P、Q同时出发,设t秒时P、Q之间的距离恰好等于2.分两种情况:
①点P、Q相遇之前,
由题意得3t+2+5t=22,解得t=2.5;
②点P、Q相遇之后,
由题意得3t﹣2+5t=22,解得t=3.
答:若点P、Q同时出发,2.5或3秒时P、Q之间的距离恰好等于2;
(3)设点P运动x秒时,在点C处追上点Q,
![]()
则AC=5x,BC=3x,
∵AC﹣BC=AB,
∴5x﹣3x=22,
解得:x=11,
∴点P运动11秒时追上点Q;
(4)线段MN的长度不发生变化,都等于11;理由如下:
①当点P在点A、B两点之间运动时:
![]()
MN=MP+NP=![]() AP+
AP+![]() BP=
BP=![]() (AP+BP)=
(AP+BP)=![]() AB=
AB=![]() ×22=11;
×22=11;
②当点P运动到点B的左侧时:
![]()
MN=MP﹣NP=![]() AP﹣
AP﹣![]() BP=
BP=![]() (AP﹣BP)=
(AP﹣BP)=![]() AB=11,
AB=11,
∴线段MN的长度不发生变化,其值为11.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的一边长为2,周长为8,那么它的腰长为 ( )
A. 2 B. 3 C. 2或3 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8.
(1)求DE的长;
(2)求△ADB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1所示,将一副三角尺的直角顶点重合在点O处.
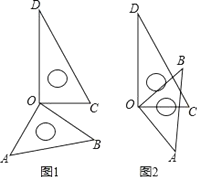
①∠AOC与∠BOD相等吗?说明理由;
②∠AOD与∠BOC数量上有什么关系吗?说明理由.
(2)若将这副三角尺按图2所示摆放,直角顶点重合在点O处,不添加字母,分析图中现有标注字母所表示的角;
①找出图中相等关系的角;
②找出图中互补关系的角,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“震灾无情人有情”.民政局将全市为四川受灾地区捐赠的物资打包成件,其中帐篷和食品共320件,帐篷比食品多80件.
(1)求打包成件的帐篷和食品各多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批帐篷和食品全部运往受灾地区.已知甲种货车最多可装帐篷40件和食品10件,乙种货车最多可装帐篷和食品各20件.则民政局安排甲、乙两种货车时有几种方案?请你帮助设计出来.
(3)在第(2)问的条件下,如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元.民政局应选择哪种方案可使运输费最少?最少运输费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,二次函数y=x2+mx+2m﹣7的图象经过点(1,0).
(1)求抛物线的表达式;
(2)把﹣4<x<1时的函数图象记为H,求此时函数y的取值范围;
(3)在(2)的条件下,将图象H在x轴下方的部分沿x轴翻折,图象H的其余部分保持不变,得到一个新图象M.若直线y=x+b与图象M有三个公共点,求b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,点A(0,3),点B(﹣3,0),点C(1,0),点D(0,1),连AB,AC,BD.
(1)求证:BD⊥AC;
(2)如图②,将△BOD绕着点O旋转,得到△B′OD′,当点D′落在AC上时,求AB′的长;
(3)试直接写出(Ⅱ)中点B′的坐标.

相关试题

