【题目】如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8.
(1)求DE的长;
(2)求△ADB的面积.

参考答案:
【答案】(1)3;(2)15
【解析】
(1)根据勾股定理求出AB,根据角平分线的性质得到CD=DE,根据三角形的面积公式求出DE;
(2)根据三角形的面积公式计算.
(1)∵在Rt△ABC中,∠C=90°,AC=6,BC=8
∴AB=10
又∵AD平分∠CAB,DE⊥AB于E
∴DE=CD,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE=6
∴BE=AB-AE=4
BD=BC-CD=8-DE
在Rt△DEB中,BD2=DE2+BE2
即(8-DE)2=DE2+42
解得:DE=3
(2)S△ADB=![]() ×AB×DE=
×AB×DE=![]() ×10×3=15
×10×3=15
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
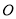 为坐标原点,菱形
为坐标原点,菱形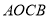 的对角线
的对角线 在
在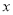 轴上,
轴上,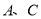 两点分别在第一象限和第四象限.直线
两点分别在第一象限和第四象限.直线 的解析式为
的解析式为 .
.
(1)如图1,求点
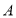 的坐标;
的坐标;(2)如图2,
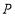 为射线
为射线 上一动点(不与点
上一动点(不与点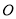 和点
和点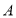 重合),过点
重合),过点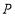 作
作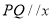 轴交直线
轴交直线 于点
于点 .设线段
.设线段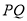 的长度为
的长度为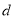 ,点
,点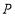 的横坐标为
的横坐标为 ,求
,求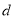 与
与 的函数关系式,并直接写出自变量
的函数关系式,并直接写出自变量 的取值范围;
的取值范围;(3)如图3,在(2)的条件下,当点
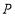 运动到线段
运动到线段 的延长线上时,连接
的延长线上时,连接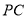 交
交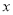 轴于点
轴于点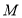 ,连接
,连接 ,
,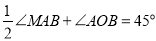 ,延长
,延长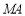 交
交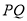 于点
于点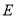 ,过
,过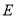 作
作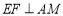 交
交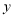 轴于点
轴于点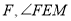 ,的角平分线
,的角平分线 交
交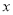 轴于点
轴于点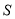 ,求点
,求点 的坐标.
的坐标. -
科目: 来源: 题型:
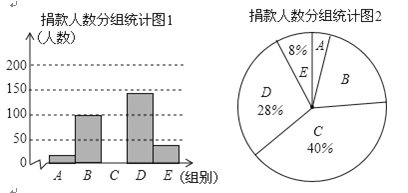
查看答案和解析>>【题目】2018年10月17日是我国第五个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整),已知A.B两组捐款人数的比为1:5.
被调查的捐款人数分组统计表:
组别
捐款额x/元
人数
A
1≤x<10
a
B
10≤x<20
100
C
20≤x<30
______
D
30≤x<40
______
E
40≤x
______
请结合以上信息解答下列问题:
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的一边长为2,周长为8,那么它的腰长为 ( )
A. 2 B. 3 C. 2或3 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1所示,将一副三角尺的直角顶点重合在点O处.
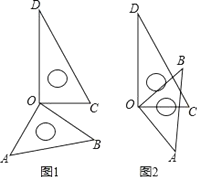
①∠AOC与∠BOD相等吗?说明理由;
②∠AOD与∠BOC数量上有什么关系吗?说明理由.
(2)若将这副三角尺按图2所示摆放,直角顶点重合在点O处,不添加字母,分析图中现有标注字母所表示的角;
①找出图中相等关系的角;
②找出图中互补关系的角,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=22,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)出数轴上点B表示的数 ;点P表示的数 (用含t的代数式表示)
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问多少秒时P、Q之间的距离恰好等于2?
(3)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?
(4)若M为AP的中点,N为BP的中点,在点P运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由,若不变,请你画出图形,并求出线段MN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“震灾无情人有情”.民政局将全市为四川受灾地区捐赠的物资打包成件,其中帐篷和食品共320件,帐篷比食品多80件.
(1)求打包成件的帐篷和食品各多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批帐篷和食品全部运往受灾地区.已知甲种货车最多可装帐篷40件和食品10件,乙种货车最多可装帐篷和食品各20件.则民政局安排甲、乙两种货车时有几种方案?请你帮助设计出来.
(3)在第(2)问的条件下,如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元.民政局应选择哪种方案可使运输费最少?最少运输费是多少元?
相关试题

