【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )
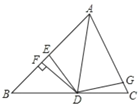
A. 6B. 12C. 4D. 8
参考答案:
【答案】A
【解析】
过点D作DH⊥AC于H,根据角平分线上的点到角的两边距离相等可得DF=DH,然后利用“HL”证明Rt△DEF和Rt△DGH全等,根据全等三角形的面积相等可得S△EDF=S△GDH,设面积为S,然后根据S△ADF=S△ADH列出方程求解即可.
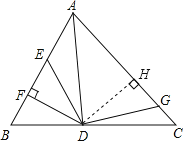 解:如图,过点D作DH⊥AC于H,
解:如图,过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,
∴DF=DH,
在Rt△DEF和Rt△DGH中,![]() ,
,
∴Rt△DEF≌Rt△DGH(HL),
∴S△EDF=S△GDH,设面积为S,
同理Rt△ADF≌Rt△ADH,
∴S△ADF=S△ADH,
即38+S=50-S,
解得S=6.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABD≌△CDB,且AB,CD是对应边.下面四个结论中不正确的是( )

A. △ABD和△CDB的面积相等B. △ABD和△CDB的周长相等
C. ∠A+∠ABD=∠C+∠CBDD. AD∥BC,且AD=BC
-
科目: 来源: 题型:
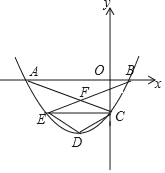
查看答案和解析>>【题目】如图,抛物线y=mx2+2mx+n经过A(﹣3,0),C(0,﹣
 )两点,与x轴交于另一点B.
)两点,与x轴交于另一点B.(1)求经过A,B,C三点的抛物线的解析式;
(2)过点C作CE∥x轴交抛物线于点E,写出点E的坐标,并求AC、BE的交点F的坐标
(3)若抛物线的顶点为D,连结DC、DE,四边形CDEF是否为菱形?若是,请证明;若不是,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,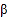 是关于
是关于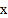 的方程
的方程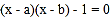 的两实根,实数
的两实根,实数 、
、 、
、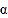 、
、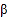 的大小关系可能是( )
的大小关系可能是( )A. α<a<b<β B. a<α<β<b C. a<α<b<β D. α<a<β<b
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
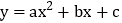 的图象如图所示,下列结论中,正确的结论的个数( )
的图象如图所示,下列结论中,正确的结论的个数( )①
 ;②
;②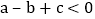 ;③
;③ ;④
;④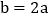 ; ⑤
; ⑤ .
.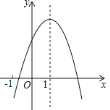
A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,在AC边上取两点M、N,使∠MBN=30°.若AM=m,MN=x,CN=n,则以x,m,n为边长的三角形的形状为( )
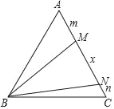
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 随x,m,n的值而定
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
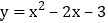 .
. (1)直接写出抛物线的开口方向、对称轴和顶点坐标;
(2)若抛物线与
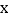 轴的两个交点为
轴的两个交点为 、
、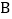 ,与
,与 轴的一个交点为
轴的一个交点为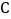 ,画草图,求
,画草图,求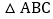 的面积.
的面积.
相关试题

