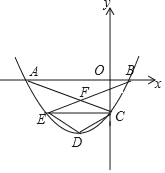
【题目】如图,抛物线y=mx2+2mx+n经过A(﹣3,0),C(0,﹣![]() )两点,与x轴交于另一点B.
)两点,与x轴交于另一点B.
(1)求经过A,B,C三点的抛物线的解析式;
(2)过点C作CE∥x轴交抛物线于点E,写出点E的坐标,并求AC、BE的交点F的坐标
(3)若抛物线的顶点为D,连结DC、DE,四边形CDEF是否为菱形?若是,请证明;若不是,请说明理由.
参考答案:
【答案】(1)y=![]() x2+x﹣
x2+x﹣![]() ;(2)F点坐标为(﹣1,﹣1);(3)四边形CDEF是菱形.证明见解析
;(2)F点坐标为(﹣1,﹣1);(3)四边形CDEF是菱形.证明见解析
【解析】
将A、C点的坐标代入抛物线的解析式中,通过联立方程组求得该抛物线的解析式;
根据(1)题所得的抛物线的解析式,可确定抛物线的对称轴方程以及B、C点的坐标,由CE∥x轴,可知C、E关于对称轴对称。根据A、C点求得直线AC的解析式,根据B、E点求出直线BE的解析式,联立方程求得的解,即为F点的坐标;
由E、C、F、D的坐标可知DF和EC互相垂直平分,则可判定四边形CDEF为菱形.
(1)∵抛物线y=mx2+2mx+n经过A(﹣3,0),C(0,﹣![]() )两点,
)两点,
∴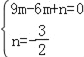 ,解得
,解得![]() ,
,
∴抛物线解析式为y=![]() x2+x﹣
x2+x﹣![]() ;
;
(2)∵y=![]() x2+x﹣
x2+x﹣![]() ,
,
∴抛物线对称轴为直线x=﹣1,
∵CE∥x轴,
∴C、E关于对称轴对称,
∵C(0,﹣![]() ),
),
∴E(﹣2,﹣![]() ),
),
∵A、B关于对称轴对称,
∴B(1,0),
设直线AC、BE解析式分别为y=kx+b,y=k′x+b′,
则由题意可得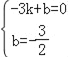 ,
,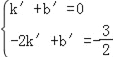 ,
,
解得![]() ,
,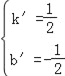 ,
,
∴直线AC、BE解析式分别为y=﹣![]() x﹣
x﹣![]() ,y=
,y=![]() x﹣
x﹣![]() ,
,
联立两直线解析式可得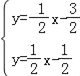 ,解得
,解得![]() ,
,
∴F点坐标为(﹣1,﹣1);
(3)四边形CDEF是菱形.
证明:∵y=![]() x2+x﹣
x2+x﹣![]() =
=![]() (x+1)2﹣2,
(x+1)2﹣2,
∴D(﹣1,﹣2),
∵F(﹣1,﹣1),
∴DF⊥x轴,且CE∥x轴,
∴DF⊥CE,
∵C(0,﹣![]() ),且F(﹣1,﹣1),D(﹣1,﹣2),
),且F(﹣1,﹣1),D(﹣1,﹣2),
∴DF和CE互相平分,
∴四边形CDEF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】温度与我们的生活息息相关,如图是一个温度计实物示意图,左边的刻度是摄氏温度(℃),右边的刻度是华氏温度(℉).设摄氏温度为x(℃)华氏温度为y(℉),则y是x的一次函数,通过观察我们发现,温度计上的摄氏温度为0℃时,华氏温度为32℉;摄氏温度为﹣20℃时,华氏温度为﹣4℉

请根据以上信息,解答下列问题
(1)仔细观察图中数据,试求出y与x的函数关系式;
(2)当摄氏温度为﹣5℃时,华氏温度为多少?
(3)当华氏温度为59℉时,摄氏温度为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(知识重现)我们知道,在ax=N中,已知底数a,指数x,求幂N的运算叫做乘方运算.例如23=8;已知幂N,指数x,求底数a的运算叫做开方运算,例如
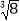 =2;
=2;(学习新知)
现定义:如果ax=N(a>0且a≠1),即a的x次方等于N(a>0且a≠1),那么数x叫做以a为底N的对数(logarithm),记作x=logaN.其中a叫做对数的底数,N叫做真数,x叫做以a为底N的对数.例如log28=3.零没有对数;在实数范围内,负数没有对数.
(应用新知)
(1)填空:在ax=N,已知幂N,底数a(a>0且a≠1),求指数x的运算叫做_____运算;
(2)选择题:在式子log5125中,真数是_____
A.3 B.5 C.10 D.125
(3)①计算以下各对数的值:log39;log327;log3243.
②根据①中计算结果,请你直接写出logaM,logaN,loga(MN)之间的关系.(其中a>0且a≠1,M>0,N>0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABD≌△CDB,且AB,CD是对应边.下面四个结论中不正确的是( )

A. △ABD和△CDB的面积相等B. △ABD和△CDB的周长相等
C. ∠A+∠ABD=∠C+∠CBDD. AD∥BC,且AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
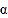 ,
,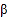 是关于
是关于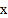 的方程
的方程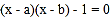 的两实根,实数
的两实根,实数 、
、 、
、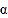 、
、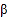 的大小关系可能是( )
的大小关系可能是( )A. α<a<b<β B. a<α<β<b C. a<α<b<β D. α<a<β<b
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )
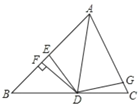
A. 6B. 12C. 4D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
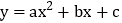 的图象如图所示,下列结论中,正确的结论的个数( )
的图象如图所示,下列结论中,正确的结论的个数( )①
 ;②
;②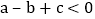 ;③
;③ ;④
;④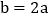 ; ⑤
; ⑤ .
.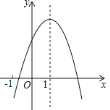
A. 5个 B. 4个 C. 3个 D. 2个
相关试题

