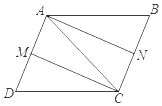
【题目】已知:如图,在平行四边形ABCD中,M、N分别是AD和BC的中点.
(1)求证:四边形AMCN是平行四边形;
(2)若AC=CD,求证四边形AMCN是矩形;
(3)若∠ACD=90°,求证四边形AMCN是菱形;
(4)若AC=CD,∠ACD=90°,求证四边形AMCN是正方形.
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析;(4)见解析.
【解析】
(1)根据平行四边形的判定定理即可得到结论;
(2)根据矩形的判定定理即可得到结论;
(3)根据菱形的判定定理即可得到结论;
(4)根据正方形的判定定理即可得到结论.
(1)由已知得AD∥BC,AD=BC,
∵M、N分别是AD和BC的中点,
∴![]()
∵AM∥CN,AM=CN,
∴四边形AMCN是平行四边形;
(2)∵AC=CD,M是AD的中点,
∴∠AMC=90°,
∵由(1)知,四边形AMCN是平行四边形,
∴四边形AMCN是矩形;
(3)∵∠ACD=90°,M是AD的中点,
∴AM=CM,
∵由(1)知,四边形AMCN是平行四边形,
∴四边形AMCN是菱形;
(4)∵AC=CD,M是AD的中点,
∴∠AMC=90°,
∵由(1)知四边形AMCN是平行四边形,
∴四边形AMCN是矩形,
∵∠ACD=90°,M是AD的中点,
∴AM=CM,
∴四边形AMCN是菱形,
∴四边形AMCN是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上
 点表示数
点表示数 ,
, 点表示数
点表示数 ,
, 点表示数
点表示数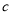 ,且
,且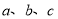 满足
满足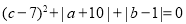 .
.(1)
 ,
,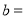 ,
,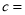 .
.(2)若将数轴折叠,使得
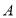 点与
点与 点重合,则点
点重合,则点 与表示 的数的点重合;
与表示 的数的点重合;(3)点
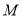 以每秒3个单位长度的速度从点
以每秒3个单位长度的速度从点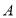 向右运动.点
向右运动.点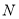 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点 向右运动(点
向右运动(点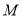 、点
、点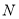 同时出发),经过几秒,点
同时出发),经过几秒,点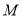 、点
、点 分别到点
分别到点 的距离相等?
的距离相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知港口A东偏南10°方向有一处小岛B,一艘货轮从港口A沿南偏东40°航线出发,行驶80海里到达C处,此时观测小岛B在北偏东60°方向.
(1)求此时货轮到小岛B的距离.
(2)在小岛周围36海里范围内是暗礁区,此时轮船向正东方向航行有没有触礁危险?请作出判断并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),B(3,0).下列结论:①2a﹣b=0;②(a+c)2<b2;③当﹣1<x<3时,y<0;④当a=1时,将抛物线先向上平移2个单位,再向右平移1个单位,得到抛物线y=(x﹣2)2﹣2.其中正确的是( )
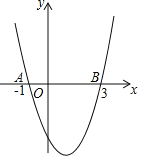
A. ①③ B. ②③ C. ②④ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC顶点B的坐标为(8,3),定点D的坐标为(12,0),动点P从点C出发.以每秒1个单位长度的速度沿CB匀速运动,动点Q从点D出发,以每秒2个单位长度的速度沿x轴的负方向匀速运动,P,Q两点同时运动,当Q点到达O点时两点同时停止运动.设运动时间为t秒,
(1)当t为何值时,四边形OCPQ为矩形?
(2)当t为何值时,以C,P,Q,A为顶点的四边形为平行四边形?
(3)E点坐标(5,0),当△OEP为等腰三角形时,请直接写出所有符合条件的点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8cm,BC=6cm,点P从点A出发,以lcm/s的速度沿A→D→C方向匀速运动,同时点Q从点A出发,以2cm/s的速度沿A→B→C方向匀速运动,当一个点到达点C时,另一个点也随之停止.设运动时间为t(s),△APQ的面积为S(cm2),下列能大致反映S与t之间函数关系的图象是( )
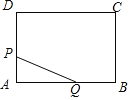
A.
 B.
B. 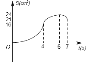 C.
C. 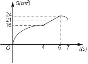 D.
D. 
-
科目: 来源: 题型:
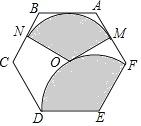
查看答案和解析>>【题目】如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1:r2=_____.
相关试题

