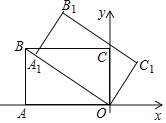
【题目】如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2![]() ).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
参考答案:
【答案】(-2![]() ,6)
,6)
【解析】
连接OB1,作B1H⊥OA于H,证明△AOB≌△HB1O,得到B1H=OA=6,OH=AB=2![]() ,得到答案.
,得到答案.
连接OB1,作B1H⊥OA于H,
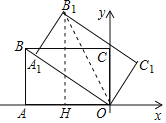
由题意得,OA=6,AB=OC-2![]() ,
,
则tan∠BOA=![]() ,
,
∴∠BOA=30°,
∴∠OBA=60°,
由旋转的性质可知,∠B1OB=∠BOA=30°,
∴∠B1OH=60°,
在△AOB和△HB1O,
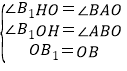 ,
,
∴△AOB≌△HB1O,
∴B1H=OA=6,OH=AB=2![]() ,
,
∴点B1的坐标为(-2![]() ,6),
,6),
故答案为:(-2![]() ,6).
,6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BE、CE 分别是∠ABC 和∠ACB 的平分线,过点 E 作 DF∥BC,交 AB 于 D,交 AC 于 F,若 AB=5,AC=4,则△ADF周长为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的面积是2平方厘米,△BCD 的面积是3平方厘米,△CDE的面积是3平方厘米,△DEF 的面积是4平方厘米,△EFG的面积是3平方厘米,△FGH的面积是5平方厘米,那么,△EFH的面积是______平方厘米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是边长为3的正方形,点E在边AD所在的直线上,连接CE,以CE为边,作正方形CEFG(点C、E、F、G按逆时针排列),连接BF.
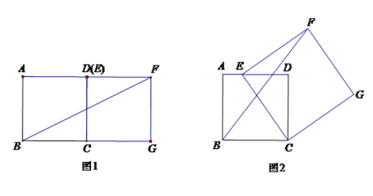
(1)如图1,当点E与点D重合时,BF的长为 ;
(2)如图2,当点E在线段AD上时,若AE=1,求BF的长;(提示:过点F作BC的垂线,交BC的延长线于点M,交AD的延长线于点N.)
(3)当点E在直线AD上时,若AE=4,请直接写出BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=2,BC=5,点D是BC边上一点且CD=1,点P是线段DB上一动点,连接AP,以AP为斜边在AP的下方作等腰Rt△AOP.当P从点D出发运动至点B停止时,点O的运动路径长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在五边形
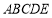 中,
中,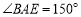 ,
,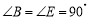 ,
,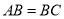 ,
,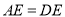 在
在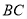 ,
,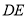 上分别找一点
上分别找一点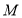 ,
,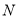 ,使得
,使得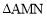 的周长最小时,则
的周长最小时,则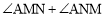 的度数为( ).
的度数为( ).
A.
 B.
B. 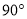 C.
C. 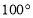 D.
D. 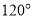
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.

(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;
(2)将图①中的三角板OMN绕点O按逆时针方向旋转至如图③,当∠CON=5∠DOM时,MN与CD相交于点E,请你判断MN与BC的位置关系,并求∠CEN的度数;
(3)将图①中的三角板OMN绕点O按每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,三角板MON运动几秒后直线MN恰好与直线CD平行.
(4)将如图①位置的两块三角板同时绕点O逆时针旋转,速度分别每秒20°和每秒10°,当其中一个三角板回到初始位置时,两块三角板同时停止转动.经过___________秒后边OC与边ON互相垂直.(直接写出答案)
相关试题

