搜索
【题目】已知k为任意实数，随着k的变化，抛物线y=x2﹣2（k﹣1）x+k2﹣3的顶点随之运动，则顶点运动时经过的路径与两条坐标轴围成图形的面积是（ ）
A. 1 B. 
C. 2 D. 
参考答案：
【答案】A
【解析】
利用配方法求出顶点坐标，得出顶点在直线y=2x﹣2上运动，由此即可解决问题．
∵y=x2﹣2（k﹣1）x+k2﹣3
=（x﹣k+1）2+k2﹣3﹣（k﹣1）2
=（x﹣k+1）2+2k﹣4
∴顶点的坐标为（k﹣1，2k﹣4）即[（k﹣1），2（k﹣1）﹣2]，∴顶点在直线y=2x﹣2上运动，易知直线y=2x﹣2交x轴于A（1，0），交y轴于B（0，﹣2），∴S△AOB=
×2×1=1，∴顶点运动时经过的路径与两条坐标轴围成图形的面积是1．
故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F，切点为G，连接AG交CD于K．
（1）如图1，求证：KE=GE；
（2）如图2，连接CABG，若∠FGB=
∠ACH，求证：CA∥FE；（3）如图3，在（2）的条件下，连接CG交AB于点N，若sinE=
，AK=
，求CN的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AB=DE，AC=DF，BF=EC
（1）求证：△ABC≌△DEF；
（2）若
，求BF的长；（3）∠B=60°，∠D=70°，求∠AGD.
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线
经过点A（
，0），B（
，0），且与y轴相交于点C．（1）求这条抛物线的表达式；
（2）求∠ACB的度数；
（3）设点D是所求抛物线第一象限上一点，且在对称轴的右侧，点E在线段AC上，且DE⊥AC，当△DCE与△AOC相似时，求点D的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点D在AB上，点E在AC上，BE、CD相交于点O.
（1）三角形的外角等于与它不相邻的两个内角的______，若∠A=45°，∠B=30°，则∠BEC=______；
（2）若∠A=50°，∠BOD=70°，∠C=30°，求∠B的度数；
（3）试猜想∠BOC与∠A、∠B、∠C之间的关系，并证明你猜想的正确性。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，已知AB⊥BD,ED⊥BD,AB=CD,BC=DE
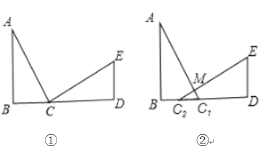
（1）求证：△ABC≌△CDE
（2）试判断AC与CE的位置关系，并说明理由．
（3）若将CD沿CB方向平移得到图②的情形，其余条件不变，此时第（2）问中AC与CE的位置关系还成立吗？请说明理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AO平分∠BAC，AO⊥BC，DE⊥BC，GH⊥BC，垂足分别为O、E、H，且DO∥AC，∠B=43°，则图中角的度数为47°的角的个数是（ ）
A. 5 B. 6 C. 7 D. 8
相关试题
