【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

参考答案:
【答案】(1)![]() ;(2)45°;(3)
;(2)45°;(3)![]() .
.
【解析】试题分析: ![]() 把点
把点![]() 的坐标代入即可求得抛物线的解析式.
的坐标代入即可求得抛物线的解析式.
![]() 作BH⊥AC于点H,求出
作BH⊥AC于点H,求出![]() 的长度,即可求出∠ACB的度数.
的长度,即可求出∠ACB的度数.
![]() 延长CD交x轴于点G,△DCE∽△AOC,只可能∠CAO=∠DCE.求出直线
延长CD交x轴于点G,△DCE∽△AOC,只可能∠CAO=∠DCE.求出直线![]() 的方程,和抛物线的方程联立即可求得点
的方程,和抛物线的方程联立即可求得点![]() 的坐标.
的坐标.
试题解析:(1)由题意,得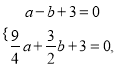
解得![]() .
.
∴这条抛物线的表达式为![]() .
.
(2)作BH⊥AC于点H,
∵A点坐标是(-1,0),C点坐标是(0,3),B点坐标是(![]() ,0),
,0),
∴AC=![]() ,AB=
,AB=![]() ,OC=3,BC=
,OC=3,BC=![]() .
.
∵![]() ,即∠BAD=
,即∠BAD= ![]() ,
,
∴![]() .
.
Rt△ BCH中, ![]() ,BC=
,BC=![]() ,∠BHC=90,
,∠BHC=90,
∴![]() .
.
又∵∠ACB是锐角,∴![]() .
.
(3)延长CD交x轴于点G,
∵Rt△ AOC中,AO=1,AC=![]() ,
,
∴![]() .
.
∵△DCE∽△AOC,∴只可能∠CAO=∠DCE.
∴AG = CG.
∴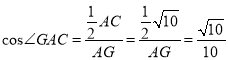 .
.
∴AG=5.∴G点坐标是(4,0).
∵点C坐标是(0,3),∴![]() .
.
∴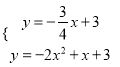 解得
解得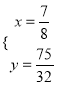 ,
, ![]() (舍).
(舍).
∴点D坐标是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发,以每秒4cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足△BCP的周长为14cm,求此时t的值;
(2)若点P在∠BAC的平分线上,求此时t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ABC=90°,AB=BC.直线l与以BC为直径的圆O相切于点C.点F是圆O上异于B、C的动点,直线BF与l相交于点E,过点F作AF的垂线交直线BC与点D.
(1)如果BE=15,CE=9,求EF的长;
(2)证明:①△CDF∽△BAF;②CD=CE;
(3)探求动点F在什么位置时,相应的点D位于线段BC的延长线上,且使BC=
 CD,请说明你的理由.
CD,请说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AB为半圆O的直径,半径的长为4cm,点C为半圆上一动点,过点C作CE⊥AB,垂足为点E,点D为弧AC的中点,连接DE,如果DE=2OE,求线段AE的长.
小何根据学习函数的经验,将此问题转化为函数问题解决.
小华假设AE的长度为xcm,线段DE的长度为ycm.
(当点C与点A重合时,AE的长度为0cm),对函数y随自变量x的变化而变化的规律进行探究.
下面是小何的探究过程,请补充完整:(说明:相关数据保留一位小数).
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm
0
1
2
3
4
5
6
7
8
y/cm
0
1.6
2.5
3.3
4.0
4.7
5.8
5.7
当x=6cm时,请你在图中帮助小何完成作图,并使用刻度尺度量此时线段DE的长度,填写在表格空白处:
(2)在图2中建立平面直角坐标系,描出补全后的表中各组对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象解决问题,当DE=2OE时,AE的长度约为 cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=4,AC=3,BC=5,DE是BC的垂直平分线,DE分别交BC、AB于点D、E.
(1)求证:△ABC为直角三角形.
(2)求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 中,
中,  ,
,  ,
,  ,D是AB边的中点,E是AC边上一点,联结DE,过点D作
,D是AB边的中点,E是AC边上一点,联结DE,过点D作 交BC边于点F,联结EF.
交BC边于点F,联结EF.(1)如图1,当
 时,求EF的长;
时,求EF的长;(2)如图2,当点E在AC边上移动时,
 的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出
的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出 的正切值;
的正切值;(3)如图3,联结CD交EF于点Q,当
 是等腰三角形时,请直接写出BF的长.
是等腰三角形时,请直接写出BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
相关试题

