【题目】如图,四边形ABCD是平行四边形,点A(2,0),B(6,2),C(6,6),反比例函数y1=![]() (x>0)的图象过点D,点P是一次函数y2=kx+3﹣3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:
(x>0)的图象过点D,点P是一次函数y2=kx+3﹣3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:
①反比例函数的解析式是y1=![]() ;
;
②一次函数y2=kx+3﹣3k(k≠0)的图象一定经过(6,6)点;
③若一次函数y2=kx+3﹣3k的图象经过点C,当x>2![]() 时,y1<y2;
时,y1<y2;
④对于一次函数y2=kx+3﹣3k(k≠0),当y随x的增大而增大时,点P横坐标a的取值范围是0<a<3.
其中正确的是( )
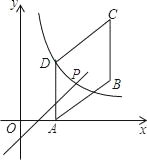
A. ①③ B. ②③ C. ②④ D. ③④
参考答案:
【答案】D
【解析】分析:①根据平行四边形的性质求D点的坐标;(2)把x=6代入y2=kx+3﹣3k中,看函数值是否为6;③把点C的坐标代入y2=kx+3﹣3k,求得一次函数的解析,由一次函数的解析式和反比例函数的解析组成的方程组可求得它们的交点坐标,结合函数图象判断;④一次函数过定点(3,3),确定x=3时的函数值即可.
详解:①∵四边形ABCD是平行四边形,∴AD=BC,
∵B(6,2),C(6,6),∴BC⊥x轴,AD=BC=4,而A点坐标为(2,0),
∴点D的坐标为(2,4),
∵反比例函数y1=![]() (x>0)的函数图象经过点D(2,4),
(x>0)的函数图象经过点D(2,4),
∴4=![]() ,∴m=8,
,∴m=8,
∴反比例函数的解析式为y=![]() ,①不正确;
,①不正确;
②当x=6时,y=kx+3﹣3k=6k+3﹣3k=3k+3≠6,
∴一次函数y=kx+3﹣3k(k≠0)的图象不一定过点C,②不正确;
③∵一次函数y2=kx+3﹣3k的图象经过点C,
∴6=6k+3﹣3k,解得:k=1.
∴y2=x.
联立![]() ,解得:
,解得:![]() 或
或![]() (舍去).
(舍去).
结合函数图象即可得出:
当x>![]() 时,y1<y2,③成立;
时,y1<y2,③成立;
④∵一次函数y2=kx+3﹣3k(k≠0),y随x的增大而增大,
∴k>0,∴交点P在第一象限.
将x=3代入到反比例函数y=![]() 中,得:y=
中,得:y=![]() .
.
∵因为y2-3=k(x﹣3),当x=3时,y2=3,
∴一次函数y2=kx+3﹣3k(k≠0)恒过点(3,3),点(3,![]() )在(3,3)的下方,
)在(3,3)的下方,
即点P应该在点(3,![]() )的左方,∴点P横坐标a的取值范围是a<3.
)的左方,∴点P横坐标a的取值范围是a<3.
即④正确.
综上可知:③④正确,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的边长是
 ,若反比例函数y=
,若反比例函数y= 的图象经过点B,则k的值为_____.
的图象经过点B,则k的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是_____.
-
科目: 来源: 题型:
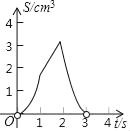
查看答案和解析>>【题目】如图,正方形ABCD的边长为3cm,点P从点A出发沿AB→BC→CD以3cm/s的速度向终点D匀速运动,同时,点Q从点A出发沿AD以1cm/s的速度向终点D匀速运动,设P点运动的时间为ts,△APQ的面积为Scm2,下列选项中能表示S与t之间函数关系的是( )
A.
 B.
B. 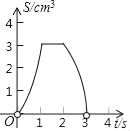
C.
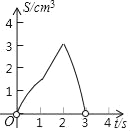 D.
D. 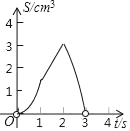
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,AC,BD是对角线,将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形;②△HED的面积是1﹣
 ;③∠AFG=112.5°;④BC+FG=
;③∠AFG=112.5°;④BC+FG= .其中正确的结论是( )
.其中正确的结论是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数
 的图象交于点A(1,6),B(3,n)两点.
的图象交于点A(1,6),B(3,n)两点.(1)求一次函数的表达式;
(2)在y轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径OD⊥弦AB于点C,连接BO并延长交⊙O于点E,连接AE,若AB=6,CD=1,则AE的长为( )
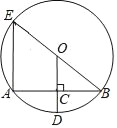
A. 3
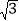 B. 8 C. 12 D. 8
B. 8 C. 12 D. 8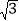
相关试题

