【题目】四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合).若四边形OBCD是平行四边形时,那么∠OBA和∠ODA的数量关系是 . 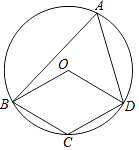
参考答案:
【答案】∠OBA﹣∠ODA=60°或∠OBA+∠ODA=60°或∠ODA﹣∠OBA=60°或∠OBA+∠ODA=120°
【解析】解: 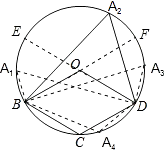
∵四边形ABCD为圆内接四边形,
∴∠A+∠C=180°.
∵四边形OBCD是平行四边形,
∴∠C=∠BOD=2∠A,
∴∠A=60°,∠C=120°.
延长DO交⊙O于点E,延长BO交⊙O于点F.
①当点A1在 ![]() 上时,
上时,
∵∠CBA1+∠CDA1=180°,∠CBO+∠CDO=360°﹣120°﹣120°=120°,
∴∠CBO+∠OBA1+∠COD﹣∠ODA1=180°,
∴∠OBA1﹣∠ODA1=60°;
②当点A2在 ![]() 上时,
上时,
∵∠CBA2+∠CDA2=180°,∠CBO+∠CDO=360°﹣120°﹣120°=120°,
∴∠CBO+∠OBA2+∠COD+∠ODA2=180°,
∴∠OBA2+∠ODA2=60°;
③当点A3在 ![]() 上时,
上时,
∵∠CBA3+∠CDA3=180°,∠CBO+∠CDO=360°﹣120°﹣120°=120°,
∴∠CBO﹣∠OBA3+∠COD+∠ODA3=180°,
∴∠ODA3﹣∠OBA3=60°;
④当点A4在 ![]() 上时,
上时,
∠OBA4+∠ODA4=360°﹣120°﹣120°=120°.
综上所述,∠OBA和∠ODA的数量关系是:∠OBA﹣∠ODA=60°或∠OBA+∠ODA=60°或∠ODA﹣∠OBA=60°或∠OBA+∠ODA=120°.
所以答案是:∠OBA﹣∠ODA=60°或∠OBA+∠ODA=60°或∠ODA﹣∠OBA=60°或∠OBA+∠ODA=120°.
【考点精析】通过灵活运用平行四边形的性质和圆周角定理,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2.则 cos∠MCN= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°.
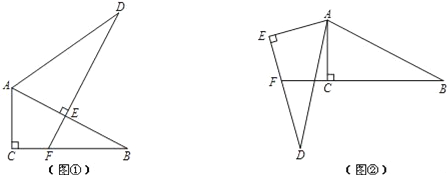
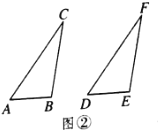
(1)将这两个三角形按图①方式摆放,使点E落在AB上,DE的延长线交BC于点F.求证:BF+EF=DE;
(2)改变△ADE的位置,使DE交BC的延长线于点F(如图②),则(1)中的结论还成立吗?若成立,加以证明;若不成立,写出此时BF、EF与DE之间的等量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习了三角形全等的判定方法和直角三角形全等的判定方法后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情况进行研究.
(初步思考)我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,
 ,然后,对
,然后,对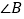 进行分类,可分为“
进行分类,可分为“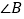 是直角,钝角,锐角”三种情况进行探索.
是直角,钝角,锐角”三种情况进行探索.(深入探究)(1)当
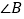 是直角时,如图①,在△ABC和△DEF中,AC=DF,BC=EF,
是直角时,如图①,在△ABC和△DEF中,AC=DF,BC=EF, ,根据 可以知道
,根据 可以知道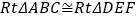 .
.(2)当
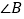 是钝角时,如图②,在△ABC和△DEF中,AC=DF,BC=EF,
是钝角时,如图②,在△ABC和△DEF中,AC=DF,BC=EF, ,且
,且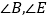 都是钝角,求证:
都是钝角,求证: .
.(3)当
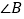 是锐角时,在△ABC和△DEF中,AC=DF,BC=EF,
是锐角时,在△ABC和△DEF中,AC=DF,BC=EF, ,且
,且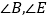 都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等(不写做法,保留作图痕迹)
都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等(不写做法,保留作图痕迹)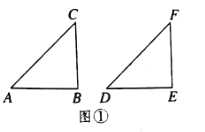

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )

A. 1组 B. 2组 C. 3组 D. 4组
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.
(1)当n=1时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性是否相同?(在答题卡相应位置填“相同”或“不相同”);
(2)从袋中随机摸出一个球,记录其颜色,然后放回,大量重复该实验,发现摸到绿球的频率稳定于0.25,则n的值是
(3)在一个摸球游戏中,所有可能出现的结果如下:
根据树状图呈现的结果,求两次摸出的球颜色不同的概率. -
科目: 来源: 题型:
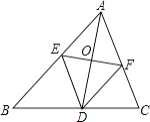
查看答案和解析>>【题目】如图,在△ABC中,AD是∠BAC的平分线,EF垂直平分AD交AB于E,交AC于F. 求证:四边形AEDF是菱形.
相关试题

