【题目】一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.
(1)当n=1时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性是否相同?(在答题卡相应位置填“相同”或“不相同”);
(2)从袋中随机摸出一个球,记录其颜色,然后放回,大量重复该实验,发现摸到绿球的频率稳定于0.25,则n的值是
(3)在一个摸球游戏中,所有可能出现的结果如下:
根据树状图呈现的结果,求两次摸出的球颜色不同的概率.
参考答案:
【答案】
(1)
解:(1)当n=1时,红球和白球的个数一样,所以被摸到的可能性相同,
故答案为:相同;
(2)2
(3)
由树状图可知,共有12种结果,其中两次摸出的球颜色不同的10种,
所以其概率=![]() =
=![]()
【解析】(1)因为红球和白球的个数一样,所以被摸到的可能性相同;
(2)根据摸到绿球的频率稳定于0.25,即可求出n的值;
(3)根据树状图即可求出两次摸出的球颜色不同的概率.
【考点精析】根据题目的已知条件,利用列表法与树状图法和用频率估计概率的相关知识可以得到问题的答案,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率;在同样条件下,做大量的重复试验,利用一个随机事件发生的频率逐渐稳定到某个常数,可以估计这个事件发生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习了三角形全等的判定方法和直角三角形全等的判定方法后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情况进行研究.
(初步思考)我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,
 ,然后,对
,然后,对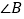 进行分类,可分为“
进行分类,可分为“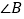 是直角,钝角,锐角”三种情况进行探索.
是直角,钝角,锐角”三种情况进行探索.(深入探究)(1)当
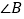 是直角时,如图①,在△ABC和△DEF中,AC=DF,BC=EF,
是直角时,如图①,在△ABC和△DEF中,AC=DF,BC=EF, ,根据 可以知道
,根据 可以知道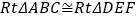 .
.(2)当
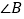 是钝角时,如图②,在△ABC和△DEF中,AC=DF,BC=EF,
是钝角时,如图②,在△ABC和△DEF中,AC=DF,BC=EF, ,且
,且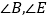 都是钝角,求证:
都是钝角,求证: .
.(3)当
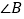 是锐角时,在△ABC和△DEF中,AC=DF,BC=EF,
是锐角时,在△ABC和△DEF中,AC=DF,BC=EF, ,且
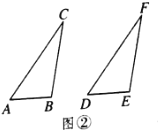
,且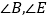 都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等(不写做法,保留作图痕迹)
都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等(不写做法,保留作图痕迹)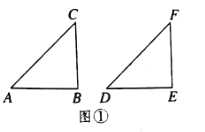

-
科目: 来源: 题型:
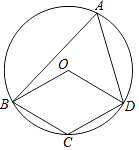
查看答案和解析>>【题目】四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合).若四边形OBCD是平行四边形时,那么∠OBA和∠ODA的数量关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )

A. 1组 B. 2组 C. 3组 D. 4组
-
科目: 来源: 题型:
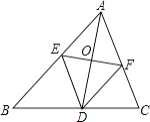
查看答案和解析>>【题目】如图,在△ABC中,AD是∠BAC的平分线,EF垂直平分AD交AB于E,交AC于F. 求证:四边形AEDF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1的小正方形组成的正方形网格中建立如图片所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形上)

(1)画出△ABC关于直线l:x=﹣1的对称三角形△A1B1C1;并写出A1、B1、C1的坐标.
(2)在直线x=﹣l上找一点D,使BD+CD最小,满足条件的D点为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】萧山北干初中组织外国教师(外教)进班上英语课,王明同学为了解全校学生对外教的喜爱程度,在全校随机抽取了若干名学生进行问卷调查.问卷将喜爱程度分为A(非常喜欢)、B(喜欢)、C(不太喜欢)、D(很不喜欢)四种类型,根据调查结果绘制成了两幅不完整的统计图,请结合统计图信息解答下列问题:
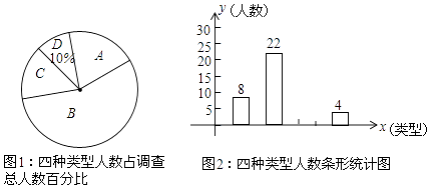
(1)这次调查中,一共调查了名学生,图1中C类所对应的圆心角度数为;
(2)请补全条形统计图;
(3)在非常喜欢外教的5位同学(三男两女)中任意抽取两位同学作为交换生,请用列表法或画树状图求出恰好抽到一名男生和一名女生作为交换生的概率.
相关试题

