【题目】某学校为了解学生课外阅读的情况,对学生“平均每天课外阅读的时间”进行了随机抽样调查,如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答以下问题: 
(1)平均每天课外阅读的时间为“0.5~1小时”部分的扇形图的圆心角为多少度;
(2)本次一共调查了多少名学生;
(3)将条形图补充完整;
(4)若该校有1680名学生,请估计该校有多少名学生平均每天课外阅读的时间在0.5小时以下.
参考答案:
【答案】
(1)解:每天课外阅读的时间为“0.5~1小时”的学生所占的比例是:1﹣50%﹣30%﹣5%=15%,
则时间为“0.5~1小时”部分的扇形图的圆心角为:15%×360°=54°,
故答案是:54;
(2)解:调查的总人数是:100÷50%=200,
故答案是:200;
(3)解:

(4)解:在0.5小时以下的人数:1680×5%=84(人).
【解析】(1)首先求出每天课外阅读的时间为“0.5~1小时”的学生所占的比例,然后乘以360°,即可求解;(2)平均每天课外阅读的时间在1~1.5小时的有100人,占50%,据此即可求得总人数;(3)利用1680人乘以所占的比例即可求解.
【考点精析】根据题目的已知条件,利用扇形统计图和条形统计图的相关知识可以得到问题的答案,需要掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.
-
科目: 来源: 题型:
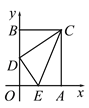
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OACB的顶点O是坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E为边OA上的一个动点,当△CDE的周长最小时,则点E的坐标____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在10×10的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的顶点上.
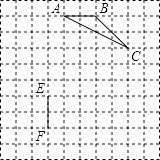
(1)填空:tanA= , AC=(结果保留根号);
(2)请你在图中找出一点D(仅一个点即可),连接DE、DF,使以D、E、F为顶点的三角形与△ABC全等,并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.
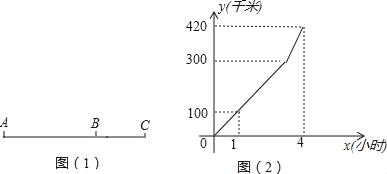
(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据图中提供的信息,回答下列问题

(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定: 这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点A表示的有理数为﹣6,点B表示的有理数为6,点P从点A出发以每秒4个单位长度的速度在数轴上由A向B运动,当点P到达点B后立即返回,仍然以每秒4个单位长度的速度运动至点A停止运动,设运动时间为t(单位:秒).
(1)求t=1时点P表示的有理数;
(2)求点P与点B重合时的t值;
(3)在点P沿数轴由点A到点B再回到点A的运动过程中,求点P与点A的距离(用含t的代数式表示);
(4)当点P表示的有理数与原点的距离是2个单位长度时,请求出所有满足条件的t值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为庆祝“六一”儿童节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校的人数多于乙校的人数,且甲校的人数不足90人)准备统一购买服装参加演出;下面是某服装厂给出的演出服装的价格表
购买服装的套数
1套至45套
46套至90套
91套以上
每套服装的价格
60元
50元
40元
(1)如果两所学校分别单独购买服装一共应付5000元,甲、乙两所学校各有多少学生准备参加演出?
(2)如果甲校有10名同学抽调去参加书法绘画比赛不能参加演出,请你为两所学校设计一种最省钱的购买服装方案.
相关试题

