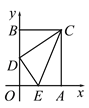
【题目】如图,在平面直角坐标系中,矩形OACB的顶点O是坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E为边OA上的一个动点,当△CDE的周长最小时,则点E的坐标____________.
参考答案:
【答案】(1,0)
【解析】分析:由于C、D是定点,则CD是定值,如果![]() 的周长最小,即
的周长最小,即![]() 有最小值.为此,作点D关于x轴的对称点D′,当点E在线段CD′上时
有最小值.为此,作点D关于x轴的对称点D′,当点E在线段CD′上时![]() 的周长最小.
的周长最小.
详解:
如图,作点D关于x轴的对称点D′,连接CD′与x轴交于点E,连接DE.
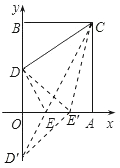
若在边OA上任取点E′与点E不重合,连接CE′、DE′、D′E′
由DE′+CE′=D′E′+CE′>CD′=D′E+CE=DE+CE,
可知△CDE的周长最小,
∵在矩形OACB中,OA=3,OB=4,D为OB的中点,
∴BC=3,D′O=DO=2,D′B=6,
∵OE∥BC,
∴Rt△D′OE∽Rt△D′BC,有![]()
∴OE=1,
∴点E的坐标为(1,0).
故答案为:(1,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年9月,莉莉进入八中初一,在准备开学用品时,她决定购买若干个某款笔记本,甲、乙两家文具店都有足够数量的该款笔记本,这两家文具店该款笔记本标价都是20元/个.甲文具店的销售方案是:购买该笔记本的数量不超过5个时,原价销售;购买该笔记本超过5个时,从第6个开始按标价的八折出售:乙文具店的销售方案是:不管购买多少个该款笔记本,一律按标价的九折出售.
(1)若设莉莉要购买x(x>5)个该款笔记本,请用含x的代数式分别表示莉莉到甲文具店和乙文具店购买全部该款笔记本所需的费用;
(2)在(1)的条件下,莉莉购买多少个笔记本时,到乙文具店购买全部笔记本所需的费用与到甲文具店购买全部笔记本所需的费用相同?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OEFG的顶点F的坐标为(4,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴上,得到矩形OMNP,OM与GF相交于点A.若经过点A的反比例函数
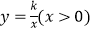 的图象交EF于点B,则点B的坐标为 .
的图象交EF于点B,则点B的坐标为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若DE=5,BD=3,则线段CE的长为( )

A. 3 B. 1 C. 2 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在10×10的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的顶点上.
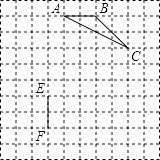
(1)填空:tanA= , AC=(结果保留根号);
(2)请你在图中找出一点D(仅一个点即可),连接DE、DF,使以D、E、F为顶点的三角形与△ABC全等,并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.
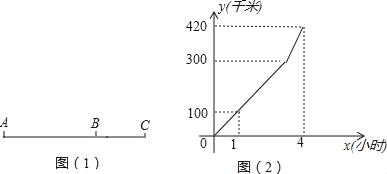
(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解学生课外阅读的情况,对学生“平均每天课外阅读的时间”进行了随机抽样调查,如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答以下问题:

(1)平均每天课外阅读的时间为“0.5~1小时”部分的扇形图的圆心角为多少度;
(2)本次一共调查了多少名学生;
(3)将条形图补充完整;
(4)若该校有1680名学生,请估计该校有多少名学生平均每天课外阅读的时间在0.5小时以下.
相关试题

