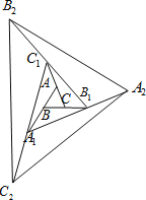
【题目】如图，△ABC的面积为1．第一次操作：分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1．第二次操作：分别延长A1B1，B1C1，C1A1至点A2，B2，C2，使A2B1=A1B1，B2C1=B1C1，C2A1=C1A1，顺次连接A2，B2，C2，得到△A2B2C2，…按此规律，要使得到的三角形的面积超过2017，最少经过（　　）次操作．

A. 6 B. 5 C. 4 D. 3

参考答案：

【答案】C

【解析】△ABC与△A1BB1底相等（AB=A1B），高为1：2（BB1=2BC），故面积比为1：2，∵△ABC面积为1，∴ =2．

同理可得， =2， =2，∴ =+++ =2+2+2+1=7；

同理可证△A2B2C2的面积=7×△A1B1C1的面积=49，第三次操作后的面积为7×49=343，第四次操作后的面积为7×343=2401．

故按此规律，要使得到的三角形的面积超过2017，最少经过4次操作．

故选C．

关闭