【题目】如图,正方形ABCD的顶点A,B与正方形EFGH的顶点G,H同在一段抛物线上,且抛物线的顶点同时落在CD和y轴上,正方形边AB与EF同时落在x轴上,若正方形ABCD的边长为4,则正方形EFGH的边长为 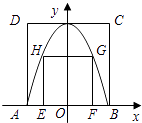
参考答案:
【答案】2 ![]() ﹣2
﹣2
【解析】解:∵正方形ABCD边长为4,
∴顶点坐标为:(0,4),B(2,0),
设抛物线解析式为:y=ax2+4,
将B点代入得,0=4a+4,
解得a=﹣1,
∴抛物线解析式为:y=﹣x2+4
设G点坐标为:(m,﹣m2+4),
则2m=﹣m2+4,
整理的:m2+2m﹣4=0,
解得:m1=﹣1+ ![]() ,a2=﹣1﹣
,a2=﹣1﹣ ![]() (不合题意舍去),
(不合题意舍去),
∴正方形EFGH的边长FG=2m=2 ![]() ﹣2.
﹣2.
所以答案是:2 ![]() ﹣2.
﹣2.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用锤子以均匀的力敲击铁钉入木板.随着铁钉的深入,铁钉所受的阻力会越来越大,使得每次钉入木板的钉子的长度后一次为前一次的k倍(0<k<1).已知一个钉子受击3次后恰好全部进入木板,且第一次受击后进入木板部分的铁钉长度是钉长的
 .设铁钉的长度为1,那么符合这一事实的方程是( )
.设铁钉的长度为1,那么符合这一事实的方程是( )
A.
(1+k)2=1
B.
k+ k2=1
k2=1
C.
+ k+
k+  k2=1
k2=1
D.
+ (1+k)2=1
(1+k)2=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】利用平方根去根号可以构造一个整系数方程.例如:x=
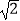 +1时,移项得x﹣1=
+1时,移项得x﹣1= 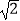 ,两边平方得(x﹣1)2=(
,两边平方得(x﹣1)2=( 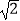 )2 , 所以x2﹣2x+1=2,即x2﹣2x﹣1=0.仿照上述构造方法,当x=
)2 , 所以x2﹣2x+1=2,即x2﹣2x﹣1=0.仿照上述构造方法,当x= 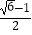 时,可以构造出一个整系数方程是( )
时,可以构造出一个整系数方程是( )
A.4x2+4x+5=0
B.4x2+4x﹣5=0
C.x2+x+1=0
D.x2+x﹣1=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An﹣1An(n为正整数),过A1 , A2 , A3 , …,An分别作x轴的平行线,与反比例函数y=
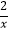 (x>0)交于点B1 , B2 , B3 , …,Bn , 如图所示的Rt△B1C1B2 , Rt△B2C2B3 , Rt△B3C3B4 , …,Rt△Bn﹣1Cn﹣1Bn面积分别记为S1 , S2 , S3 , …,Sn﹣1 , 则S1+S2+S3+…+Sn﹣1=( )
(x>0)交于点B1 , B2 , B3 , …,Bn , 如图所示的Rt△B1C1B2 , Rt△B2C2B3 , Rt△B3C3B4 , …,Rt△Bn﹣1Cn﹣1Bn面积分别记为S1 , S2 , S3 , …,Sn﹣1 , 则S1+S2+S3+…+Sn﹣1=( ) 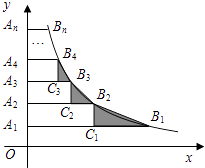
A.1
B.2
C.1﹣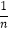
D.2﹣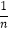
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB为⊙O的直径,AB=4.动点P从A点出发,以每秒π个单位的速度在⊙O上按顺时针方向运动一周.设动点P的运动时间为t秒,点C是圆周上一点,且∠AOC=40°,当t=秒时,点P与点C中心对称,且对称中心在直径AB上.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为-7,点B表示的数为5,点C到点A,点B的距离相等,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动的时间为
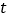 (
(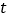 >0)秒
>0)秒(1)点C表示的数是_________.
(2)求当
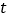 等于多少秒时,点P到达点B处.
等于多少秒时,点P到达点B处.(3)点P表示的数是_________(用含有
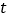 的代数式表示).
的代数式表示).(4)求当t等于多少秒时,PC之间的距离为2个单位长度(只列式,不计算).

-
科目: 来源: 题型:
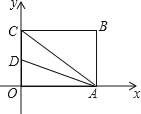
查看答案和解析>>【题目】如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(8,6),∠CAO的平分线与y轴相交于点D,则点D的坐标为_____.
相关试题

