【题目】如图,在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An﹣1An(n为正整数),过A1 , A2 , A3 , …,An分别作x轴的平行线,与反比例函数y= ![]() (x>0)交于点B1 , B2 , B3 , …,Bn , 如图所示的Rt△B1C1B2 , Rt△B2C2B3 , Rt△B3C3B4 , …,Rt△Bn﹣1Cn﹣1Bn面积分别记为S1 , S2 , S3 , …,Sn﹣1 , 则S1+S2+S3+…+Sn﹣1=( )
(x>0)交于点B1 , B2 , B3 , …,Bn , 如图所示的Rt△B1C1B2 , Rt△B2C2B3 , Rt△B3C3B4 , …,Rt△Bn﹣1Cn﹣1Bn面积分别记为S1 , S2 , S3 , …,Sn﹣1 , 则S1+S2+S3+…+Sn﹣1=( ) 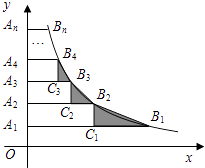
A.1
B.2
C.1﹣ ![]()
D.2﹣ ![]()
参考答案:
【答案】C
【解析】解:设OA1=A1A2=A2A3=…=An﹣1An=a,
由题意得,
B1( ![]() ,a),B2(
,a),B2( ![]() ,2a),B3(
,2a),B3( ![]() ,3a),B4(
,3a),B4( ![]() ,4a),…,Bn(
,4a),…,Bn( ![]() ,na),
,na),
则S1+S2+S3+…+Sn﹣1= ![]() ×(
×( ![]() ﹣
﹣ ![]() )×a+
)×a+ ![]() ×(
×( ![]() ﹣
﹣ ![]() )×a+
)×a+ ![]() ×(
×( ![]() ﹣
﹣ ![]() )×a+…+
)×a+…+ ![]() ×(
×( ![]() ﹣
﹣ ![]() )×a
)×a
=1﹣ ![]() ,
,
故选C.
【考点精析】解答此题的关键在于理解比例系数k的几何意义的相关知识,掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)当
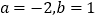 时,求两个代数式
时,求两个代数式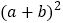 与
与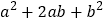 的值;
的值;(2)当
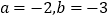 时,再求以上两个代数式的值;
时,再求以上两个代数式的值;(3)你能从上面的计算结果中,发现上面有什么结论?
结论是: ;
-
科目: 来源: 题型:
查看答案和解析>>【题目】用锤子以均匀的力敲击铁钉入木板.随着铁钉的深入,铁钉所受的阻力会越来越大,使得每次钉入木板的钉子的长度后一次为前一次的k倍(0<k<1).已知一个钉子受击3次后恰好全部进入木板,且第一次受击后进入木板部分的铁钉长度是钉长的
 .设铁钉的长度为1,那么符合这一事实的方程是( )
.设铁钉的长度为1,那么符合这一事实的方程是( )
A.
(1+k)2=1
B.
k+ k2=1
k2=1
C.
+ k+
k+  k2=1
k2=1
D.
+ (1+k)2=1
(1+k)2=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】利用平方根去根号可以构造一个整系数方程.例如:x=
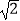 +1时,移项得x﹣1=
+1时,移项得x﹣1= 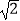 ,两边平方得(x﹣1)2=(
,两边平方得(x﹣1)2=( 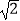 )2 , 所以x2﹣2x+1=2,即x2﹣2x﹣1=0.仿照上述构造方法,当x=
)2 , 所以x2﹣2x+1=2,即x2﹣2x﹣1=0.仿照上述构造方法,当x= 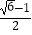 时,可以构造出一个整系数方程是( )
时,可以构造出一个整系数方程是( )
A.4x2+4x+5=0
B.4x2+4x﹣5=0
C.x2+x+1=0
D.x2+x﹣1=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的顶点A,B与正方形EFGH的顶点G,H同在一段抛物线上,且抛物线的顶点同时落在CD和y轴上,正方形边AB与EF同时落在x轴上,若正方形ABCD的边长为4,则正方形EFGH的边长为
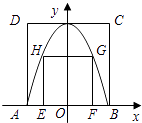
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB为⊙O的直径,AB=4.动点P从A点出发,以每秒π个单位的速度在⊙O上按顺时针方向运动一周.设动点P的运动时间为t秒,点C是圆周上一点,且∠AOC=40°,当t=秒时,点P与点C中心对称,且对称中心在直径AB上.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为-7,点B表示的数为5,点C到点A,点B的距离相等,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动的时间为
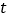 (
(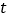 >0)秒
>0)秒(1)点C表示的数是_________.
(2)求当
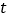 等于多少秒时,点P到达点B处.
等于多少秒时,点P到达点B处.(3)点P表示的数是_________(用含有
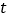 的代数式表示).
的代数式表示).(4)求当t等于多少秒时,PC之间的距离为2个单位长度(只列式,不计算).

相关试题

