搜索
【题目】利用平方根去根号可以构造一个整系数方程．例如：x= 
+1时，移项得x﹣1= ，两边平方得（x﹣1）2=（ ）2 ， 所以x2﹣2x+1=2，即x2﹣2x﹣1=0．仿照上述构造方法，当x= 
时，可以构造出一个整系数方程是（ ）
A.4x2+4x+5=0
B.4x2+4x﹣5=0
C.x2+x+1=0
D.x2+x﹣1=0
参考答案：
【答案】B
【解析】解：由题意可得：x= 
，
可变形为：2x= 
﹣1，
则（2x+1）= ，
故（2x+1）2=6，
则可以构造出一个整系数方程是：4x2+4x﹣5=0．
故选：B．
【考点精析】本题主要考查了一元二次方程的定义的相关知识点，需要掌握只有一个未知数，并且未知数的项的最高系数为2的方程为一元二次方程才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】平面上，矩形ABCD与直径为QP的半圆K如图1摆放，分别延长DA和QP交于点O，且∠DOQ=60°，OQ=0D=3，OP=2，OA=AB=1．让线段OD及矩形ABCD位置固定，将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转，设旋转角为α（0°≤α≤60°）．
发现：
（1）当α=0°，即初始位置时，点P直线AB上．（填“在”或“不在”）求当α是多少时，OQ经过点B．
（2）在OQ旋转过程中，简要说明α是多少时，点P，A间的距离最小？并指出这个最小值；
（3）如图2，当点P恰好落在BC边上时，求a及S阴影
拓展：
如图3，当线段OQ与CB边交于点M，与BA边交于点N时，设BM=x（x＞0），用含x的代数式表示BN的长，并求x的取值范围．
探究：当半圆K与矩形ABCD的边相切时，求sinα的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）当
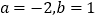时，求两个代数式
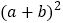与
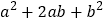的值；（2）当
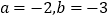时，再求以上两个代数式的值；（3）你能从上面的计算结果中，发现上面有什么结论？
结论是： ；
-
科目： 来源： 题型：
查看答案和解析>>【题目】用锤子以均匀的力敲击铁钉入木板．随着铁钉的深入，铁钉所受的阻力会越来越大，使得每次钉入木板的钉子的长度后一次为前一次的k倍（0＜k＜1）．已知一个钉子受击3次后恰好全部进入木板，且第一次受击后进入木板部分的铁钉长度是钉长的
．设铁钉的长度为1，那么符合这一事实的方程是（ ）
A.
（1+k）2=1
B.
k+ k2=1
C.
+ k+ k2=1
D.
+ （1+k）2=1 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An﹣1An（n为正整数），过A1 ， A2 ， A3 ， …，An分别作x轴的平行线，与反比例函数y=
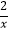（x＞0）交于点B1 ， B2 ， B3 ， …，Bn ， 如图所示的Rt△B1C1B2 ， Rt△B2C2B3 ， Rt△B3C3B4 ， …，Rt△Bn﹣1Cn﹣1Bn面积分别记为S1 ， S2 ， S3 ， …，Sn﹣1 ， 则S1+S2+S3+…+Sn﹣1=（ ）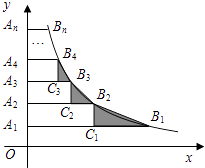 
A.1
B.2
C.1﹣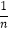
D.2﹣ -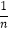
科目： 来源： 题型：
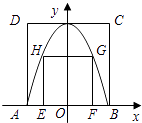
查看答案和解析>>【题目】如图，正方形ABCD的顶点A，B与正方形EFGH的顶点G，H同在一段抛物线上，且抛物线的顶点同时落在CD和y轴上，正方形边AB与EF同时落在x轴上，若正方形ABCD的边长为4，则正方形EFGH的边长为
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在⊙O中，AB为⊙O的直径，AB=4．动点P从A点出发，以每秒π个单位的速度在⊙O上按顺时针方向运动一周．设动点P的运动时间为t秒，点C是圆周上一点，且∠AOC=40°，当t=秒时，点P与点C中心对称，且对称中心在直径AB上．
相关试题
