【题目】已知在纸面上有一数轴(如图所示),
![]()
操作一:(1)折叠纸面,使1表示的点与1表示的点重合,回答一下问题:
①2表示的点与______表示的点重合;②π表示的点与______表示的点重合。
操作二:(2)折叠纸面,使1表示的点与3表示的点重合,回答以下问题:
①5表示的点与数_____表示的点重合;②![]() 表示的点与数_____表示的点重合
表示的点与数_____表示的点重合
操作三:(3)已知在数轴上点A表示的数是a,点A移动5个单位,此时点A表示的数和a是互为相反数,求a的值.
参考答案:
【答案】 2 -π -3 ![]()
【解析】试题分析:
(1)由题意可知,折叠后重合在一起的点在数轴上到原点的距离相等,由此可得答案;
(2)由题意可知,折叠后重合在一起的点在数轴上到表示1的点的距离相等,由此可得答案;
(3)题中没有指明点A移动的方向,因此要分点A向左和向右移动两种情况进行分析,再根据题意可知移动前后两个点表示的数的和为0,列方程即可求解.
试题解析:
(1)由题意可知:当折叠纸面后,表示1的点与表示-1的点重合时,表示-2的点与表示2的点重合,表示![]() 的点与表示
的点与表示![]() 的点重合;
的点重合;
(2)由题意可知:折叠纸面后,表示-1的点与表示3的点重合时,表示5的点会与表示-3的点重合,表示![]() 的点会与表示
的点会与表示![]() 的点重合;
的点重合;
(3)如果点A是向左移动的,由题意可得: ![]() ,解得
,解得![]() ;
;
如果点A是向右移动,由题意可得: ![]() ,解得
,解得![]() .
.
∴当点A移动5个单位,新数与原数互为相反数时, ![]() 的值为2.5或-2.5.
的值为2.5或-2.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“十·一”黄金周期间,武汉动物园在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期
10月1日
10月2日
10月3日
10月4日
10月5日
10月6日
10月7日
人数变化单位:万人
+1.6
+0.8
+0.4
-0.4
-0.8
+0.2
-1.2
(1)若9月30日的游客人数记为
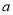 ,请用
,请用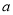 的代数式表示10月2日的游客人数?
的代数式表示10月2日的游客人数?(2)请判断七天内游客人数最多的是哪天?请说明理由。
(3)若9月30日的游客人数为2万人,门票每人10元。问黄金周期间武汉动物园门票收入是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a、b是两个整数,若定义一种运算“△”,a△b=a2+b2+ab,则方程(x+2)△x=1的实数根是( )
A. x1=x2=1B. x1=0,x2=1
C. x1=x2=﹣1D. x1=1,x2=﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:4x2y﹣y3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明有5张写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题:

(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小值是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算式子:
-
科目: 来源: 题型:
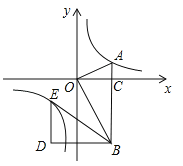
查看答案和解析>>【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(
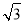 ,1)在反比例函数
,1)在反比例函数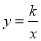 的图象上.
的图象上.(1)求反比例函数
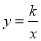 的表达式;
的表达式;(2)在x轴的负半轴上存在一点P,使得S△AOP=
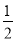 S△AOB,求点P的坐标;
S△AOB,求点P的坐标;(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
-
科目: 来源: 题型:
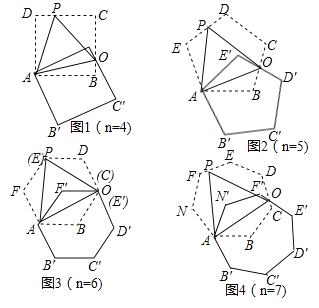
查看答案和解析>>【题目】如图,将正n边形绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为“叠弦角”,△AOP为“叠弦三角形”.
【探究证明】
(1)请在图1和图2中选择其中一个证明:“叠弦三角形”(△AOP)是等边三角形;
(2)如图2,求证:∠OAB=∠OAE′.
【归纳猜想】
(3)图1、图2中的“叠弦角”的度数分别为 , ;
(4)图n中,“叠弦三角形” 等边三角形(填“是”或“不是”)
(5)图n中,“叠弦角”的度数为 (用含n的式子表示)
相关试题

