【题目】小明有5张写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题:
![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小值是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算式子:
参考答案:
【答案】(1)15;(2)![]() ;(3)方法不唯一
;(3)方法不唯一
【解析】试题分析:(1)观察这五个数,要找乘积最大的就要找符号相同且数值最大的数,所以选-3和-5;
(2)2张卡片上数字相除的商最小就要找符号不同,且分母越大越好,分子越小越好,所以就要选3和-5,且-5为分母;
(3)从中取出4张卡片,用学过的运算方法,使结果为24,这就不唯一,用加减乘除只要答数是24即可,比如-3、-5、0、3,四个数,{0-[(-3)+(-5)]}×3=24,再如:抽取-3、-5、3、4,则-[(-3)÷3+(-5)]×4=24.
试题解析:(1)(-3) ×(-5)=15;
(2)(5)÷(+3)= ![]() ;
;
(3)方法不唯一,如:抽取3、5、0、3,则{0[(3)+(5)]}×3=24;
如:抽取3、5、3、4,则[(3)÷3+(5)]×4=24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a、b是两个整数,若定义一种运算“△”,a△b=a2+b2+ab,则方程(x+2)△x=1的实数根是( )
A. x1=x2=1B. x1=0,x2=1
C. x1=x2=﹣1D. x1=1,x2=﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:4x2y﹣y3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在纸面上有一数轴(如图所示),

操作一:(1)折叠纸面,使1表示的点与1表示的点重合,回答一下问题:
①2表示的点与______表示的点重合;②π表示的点与______表示的点重合。
操作二:(2)折叠纸面,使1表示的点与3表示的点重合,回答以下问题:
①5表示的点与数_____表示的点重合;②
 表示的点与数_____表示的点重合
表示的点与数_____表示的点重合操作三:(3)已知在数轴上点A表示的数是a,点A移动5个单位,此时点A表示的数和a是互为相反数,求a的值.
-
科目: 来源: 题型:
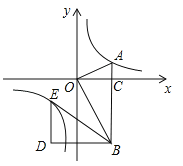
查看答案和解析>>【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(
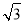 ,1)在反比例函数
,1)在反比例函数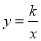 的图象上.
的图象上.(1)求反比例函数
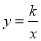 的表达式;
的表达式;(2)在x轴的负半轴上存在一点P,使得S△AOP=
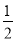 S△AOB,求点P的坐标;
S△AOB,求点P的坐标;(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
-
科目: 来源: 题型:
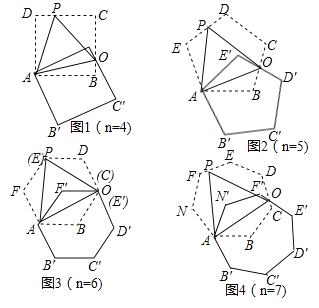
查看答案和解析>>【题目】如图,将正n边形绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为“叠弦角”,△AOP为“叠弦三角形”.
【探究证明】
(1)请在图1和图2中选择其中一个证明:“叠弦三角形”(△AOP)是等边三角形;
(2)如图2,求证:∠OAB=∠OAE′.
【归纳猜想】
(3)图1、图2中的“叠弦角”的度数分别为 , ;
(4)图n中,“叠弦三角形” 等边三角形(填“是”或“不是”)
(5)图n中,“叠弦角”的度数为 (用含n的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP= .

相关试题

