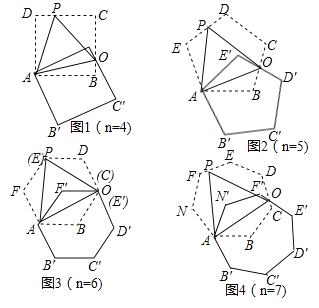
【题目】如图,将正n边形绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为“叠弦角”,△AOP为“叠弦三角形”.
【探究证明】
(1)请在图1和图2中选择其中一个证明:“叠弦三角形”(△AOP)是等边三角形;
(2)如图2,求证:∠OAB=∠OAE′.
【归纳猜想】
(3)图1、图2中的“叠弦角”的度数分别为 , ;
(4)图n中,“叠弦三角形” 等边三角形(填“是”或“不是”)
(5)图n中,“叠弦角”的度数为 (用含n的式子表示)
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)15°,24°;(4)是;(5)![]() .
.
【解析】
试题分析:(1)先由旋转的性质,再判断出△APD≌△AOD',最后用旋转角计算即可;
(2)先判断出Rt△AEM≌Rt△ABN,在判断出Rt△APM≌Rt△AON 即可;
(3)先判断出△AD′O≌△ABO,再利用正方形,正五边形的性质和旋转的性质,计算即可;
(4)先判断出△APF≌△AE′F′,再用旋转角为60°,从而得出△PAO是等边三角形;
(5)用(3)的方法求出正n边形的,“叠弦角”的度数.
试题解析:(1)如图1,∵四ABCD是正方形,由旋转知:AD=AD',∠D=∠D'=90°,∠DAD'=∠OAP=60°,∴∠DAP=∠D'AO,∴△APD≌△AOD',∴AP=AO,∵∠OAP=60°,∴△AOP是等边三角形;

(2)如图2,作AM⊥DE于M,作AN⊥CB于N.∵五ABCDE是正五边形,由旋转知:AE=AE',∠E=∠E'=108°,∠EAE'=∠OAP=60°,∴∠EAP=∠E'AO,∴△APE≌△AOE'(ASA),∴∠OAE'=∠PAE.
在Rt△AEM和Rt△ABN中,∠AEM=∠ABN=72°,AE=AB,∴Rt△AEM≌Rt△ABN (AAS),∴∠EAM=∠BAN,AM=AN.在Rt△APM和Rt△AON中,AP=AO,AM=AN,∴Rt△APM≌Rt△AON (HL),∴∠PAM=∠OAN,∴∠PAE=∠OAB,∴∠OAE'=∠OAB (等量代换).

(3)由(1)有,△APD≌△AOD',∴∠DAP=∠D′AO,在△AD′O和△ABO中,∵AD′=AB,AO=AO,∴△AD′O≌△ABO,∴∠D′AO=∠BAO,由旋转得,∠DAD′=60°,∵∠DAB=90°,∴∠D′AB=∠DAB﹣∠DAD′=30°,∴∠D′AD=![]() ∠D′AB=15°,同理可得,∠E′AO=24°,故答案为:15°,24°.
∠D′AB=15°,同理可得,∠E′AO=24°,故答案为:15°,24°.
(4)如图3,∵六边形ABCDEF和六边形A′B′C′E′F′是正六边形,∴∠F=F′=120°,由旋转得,AF=AF′,EF=E′F′,∴△APF≌△AE′F′,∴∠PAF=∠E′AF′,由旋转得,∠FAF′=60°,AP=AO
∴∠PAO=∠FAO=60°,∴△PAO是等边三角形.
故答案为:是.

(5)同(3)的方法得,∠OAB=[(n﹣2)×180°÷n﹣60°]÷2=![]() .
.
故答案:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在纸面上有一数轴(如图所示),

操作一:(1)折叠纸面,使1表示的点与1表示的点重合,回答一下问题:
①2表示的点与______表示的点重合;②π表示的点与______表示的点重合。
操作二:(2)折叠纸面,使1表示的点与3表示的点重合,回答以下问题:
①5表示的点与数_____表示的点重合;②
 表示的点与数_____表示的点重合
表示的点与数_____表示的点重合操作三:(3)已知在数轴上点A表示的数是a,点A移动5个单位,此时点A表示的数和a是互为相反数,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明有5张写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题:

(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小值是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算式子:
-
科目: 来源: 题型:
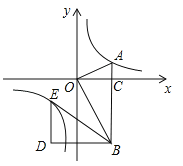
查看答案和解析>>【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(
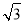 ,1)在反比例函数
,1)在反比例函数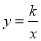 的图象上.
的图象上.(1)求反比例函数
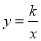 的表达式;
的表达式;(2)在x轴的负半轴上存在一点P,使得S△AOP=
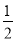 S△AOB,求点P的坐标;
S△AOB,求点P的坐标;(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】六边形的内角和是( )
A.540°
B.720°
C.900°
D.360° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.
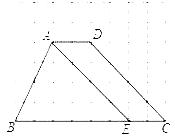
(1)在图中画出△AEF,使△AEF与△AEB关于直线AE对称,点F与点B是对称点,并求出BF的长;
(2)△AEF与四边形ABCD重叠部分的面积为 .
相关试题

