【题目】为了了解市民私家车出行的情况,某市交通管理部门对拥有私家车的市民进行随机抽样调查、其中一个问题是“你平均每天开车出行的时间是多少”共有4个选项:A、1小时以上(不含1小时);B:0.5-1小时(不含0.5小时);C:0-0.5小时(不含0小时);D,不开车.图1、2是根据调査结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
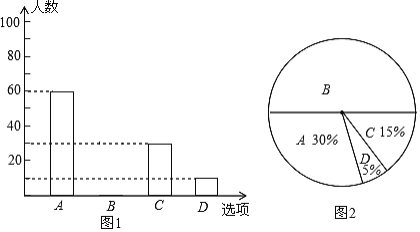
(1)本次一共调查了______名市民;
(2)在图1中将选项B的部分补充完整,并求图2中,A类所对应扇形圆心角α的度数;
(3)若该市共有200万私家车,你估计全市可能有多少私家车平均每天开车出行的时间在1小时以上?
参考答案:
【答案】(1)200;(2)见解析,108°;(3)60万.
【解析】
(1)由A选项的人数及其所占百分比可得总人数;
(2)先根据百分比之和等于1求得B的百分比,再乘以总人数即可得B选项人数,从而补全条形图;用360°乘以A选项的百分比即可得.
(3)用总数量乘以A选项的百分比即可得.
解:(1)本次调查的市民总人数为60÷30%=200(人),
故答案为:200;
(2)∵B选项对应的百分比为1-(30%+5%+15%)=50%,
∴B选项的人数为200×50%=100(人),
补全图形如下:
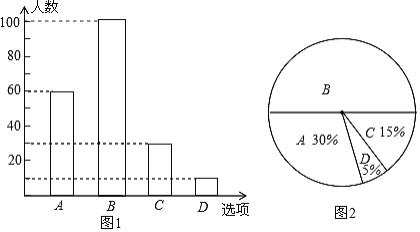
A类所对应扇形圆心角α的度数为360°×30%=108°;
(3)估计全市平均每天开车出行的时间在1小时以上私家车数量约为200×30%=60(万).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
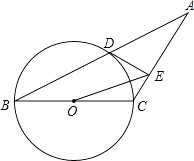
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是用火柴棍摆成边长分别是1、2、3根火柴棍时的正方形,当边长为n根火柴棍时,若摆出的正方形所用的火柴棍的根数为S,则S= (用含n的代数式表示,n为正整数).

-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,在△ABC中,AB=AC,D为BC上一点,∠B=30°,连接AD.
(1)若∠BAD=45°,求证:△ACD为等腰三角形;
(2)若△ACD为直角三角形,求∠BAD的度数.
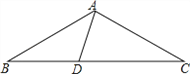
-
科目: 来源: 题型:
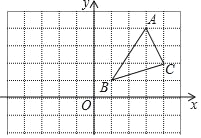
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
(1)作出△ABC关于y轴对称的△A1B1C1,并写出点C1的坐标 ;
(2)在(1)的条件下,连接CC1交AB于点D,请标出点D,并直接写出CD的长.
-
科目: 来源: 题型:
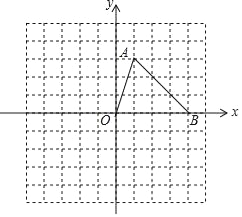
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABO的三个顶点坐标分别为A(1,3),B(4,0),O(0,0).
(1)画出将△ABO向左平移4个单位长度,再向上平移2个单位长度后得到的△A1B1O1;
(2)在(1)中,若△ABC上有一点M(3,1),则其在△A1B1O1中的对应点M1的坐标为 ;
(3)若将(1)中△A1B1O1看成是△ABO经过一次平移得到的,则这一平移的距离是 ;
(4)画出△ABO关于点O成中心对称的图形△A2B2O.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,沿折线ABCD方向以3cm/s的速度匀速运动;点Q从点D出发,沿线段DC方向以2cm/s的速度匀速运动. 已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为t(s).
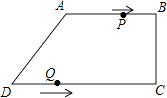
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.
相关试题

