【题目】在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,沿折线ABCD方向以3cm/s的速度匀速运动;点Q从点D出发,沿线段DC方向以2cm/s的速度匀速运动. 已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为t(s).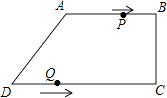
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.
参考答案:
【答案】
(1)解:如图1:过点A作AM⊥CD于点M,
∵∠BCD=90°,
即BC⊥CD,
∴AM∥BC,
又∵AB∥CD,
∴四边形ABCM为平行四边形,
∵∠BCD=90°,
∴平行四边形ABCM为矩形,
∵AB=AD=10cm,BC=8cm,
∴AM=BC=8cm,CM=AB=10cm,
在Rt△ADM中,
∴DM=![]() =6cm,
=6cm,
∴CD=CM+MD=10+6=16cm.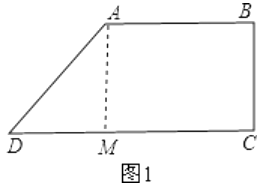
(2)解:如图2:
∵运动时间为t,
∴AP=3t,DQ=2t,
又∵AB=10cm,
∴PB=AB-AP=10-3t,
又∵四边形PBQD为平行四边形,
∴PB=DQ,
∴10-3t=2t,
∴t=2,
∴PB=DQ=4cm,
由(1)知CD=16cm,
∴CQ=12cm,
又∵BC=8cm,∠BCD=90°,
在Rt△BCQ中,
∴BQ=![]() =4
=4![]() cm,
cm,
∴CPBQD=2(PB+BQ)=2×(4+4![]() )=8+8
)=8+8![]() (cm).
(cm).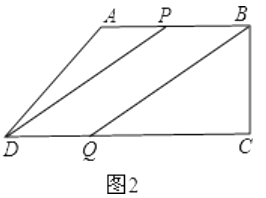
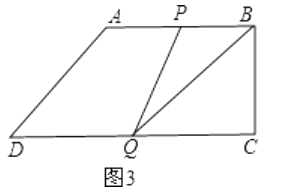
(3)解:①当P在AB上时,如图3,
∵运动时间为t,
∴AP=3t,DQ=2t,
∴0![]() 3t
3t![]() 10,
10,
∴0![]() t
t![]()
![]() ,
,
又∵AB=10cm,BC=8cm,
∴PB=AB-AP=10-3t,
∴S△BPQ=![]() .BP.BC=
.BP.BC=![]() ×(10-3t)×8=20,
×(10-3t)×8=20,
∴t=![]() .
.
②当P在BC上时,如图4,
∵运动时间为t,
∴AP=3t,DQ=2t,
∴10![]() 3t
3t![]() 18,
18,
∴![]()
![]() t
t![]() 6,
6,
又∵AB=10cm,BC=8cm,
∴PB=AB-AP=3t-10,
又由(1)知CD=16cm,
∴CQ=16-2t,
∴S△BPQ=![]() .BP.CQ=
.BP.CQ=![]() ×(3t-10)×(16-2t)=20,
×(3t-10)×(16-2t)=20,
∴3t2-34t+100=0,
∴△=342-4×3×100=-44![]() 0,
0,
∴从方程无解.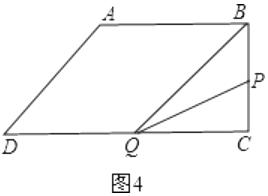
③当P在CD上时,若点P在点Q的右侧,如图5,
∵运动时间为t,
∴AP=3t,DQ=2t,
又∵AB=10cm,BC=8cm,
∴CP=AP-AB-BC=3t-18,
又由(1)知CD=16cm,
∴CQ=16-2t,
∴PQ=CQ-CP=(16-2t)-(3t-18)=34-5t,
∴![]() ,
,
∴6![]() t
t![]()
![]() .
.
∴S△BPQ=![]() .PQ.BC=
.PQ.BC=![]() ×(34-5t)×8=20,
×(34-5t)×8=20,
∴t=![]()
![]() 6(不合题意,舍去).
6(不合题意,舍去).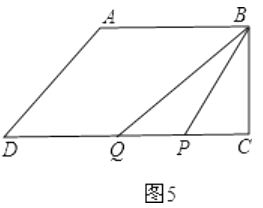
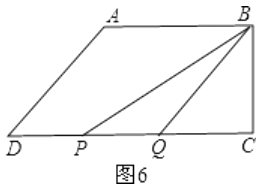
④当P在CD上时,若点P在点Q的左侧,如图6,
∵运动时间为t,
∴AP=3t,DQ=2t,
又∵AB=10cm,BC=8cm,
∴CP=AP-AB-BC=3t-18,
又由(1)知CD=16cm,
∴CQ=16-2t,
∴PQ=CP-CQ=(3t-18)-(16-2t)=5t-34,
∴![]() ,
,
∴![]()
![]() t
t![]() 8.
8.
∴S△BPQ=![]() .PQ.BC=
.PQ.BC=![]() ×(5t-34)×8=20,
×(5t-34)×8=20,
∴t=![]() .
.
综上所述:当t=![]() 秒或
秒或![]() 秒时,△BPQ的面积为20cm2.
秒时,△BPQ的面积为20cm2.
【解析】(1)如图1:过点A作AM⊥CD于点M,由∠BCD=90°,AB∥CD得出四边形ABCM为矩形,在Rt△ADM中,根据勾股定理求出DM=6cm,
从而求出CD=CM+MD=10+6=16cm.
(2)如图2:由题意得出AP=3t,DQ=2t,PB=AB-AP=10-3t,由平行四边形的性质求出t的值,从而得出PB=DQ=4cm,再由勾股定理求出
BQ的值,从而求出四边形PBQD的周长.
(3)根据题意分四种情况讨论:①当P在AB上时,如图3;②当P在BC上时,如图4;③当P在CD上时,若点P在点Q的右侧,如图5;④当P在CD上时,若点P在点Q的左侧,如图6;根据题意画出符合所有条件的图形,再由三角形的面积列出方程,求出符合范围的数值即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=2时,代数式2x4(x2+2x+2)﹣x2(4+4x3+2x4)的值是( )
A.-48
B.0
C.24
D.48 -
科目: 来源: 题型:
查看答案和解析>>【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间
(小时)
2
2.5
3
3.5
4
学生人数(名)
1
2
8
6
3
则关于这20名学生阅读小时数的说法正确的是( )
A. 众数是8 B. 中位数是3 C. 平均数是3 D. 方差是0.34
-
科目: 来源: 题型:
查看答案和解析>>【题目】将命题“等腰三角形两底角相等”改写成“如果……那么……”的形式______,它是______(填“真”或“假”)命题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(2,﹣3)关于x轴的对称点的坐标为( )
A. (﹣2,﹣3) B. (2,3) C. (﹣2,3) D. (3,﹣2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(a3)2的结果是( )
A.a9
B.a6
C.a5
D.a -
科目: 来源: 题型:
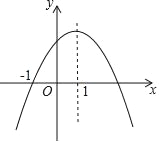
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象如图所示,下列结论:①abc<0;②2a+b<0;③b2﹣4ac=0;④8a+c<0;⑤a:b:c=﹣1:2:3,其中正确的结论有______.
相关试题

