【题目】初中生在数学运算中使用计算器的现象越来越普遍,某校一兴趣小组随机抽查了本校若干名学生使用计算器的情况.以下是根据抽查结果绘制出的不完整的条形统计图和扇形统计图: 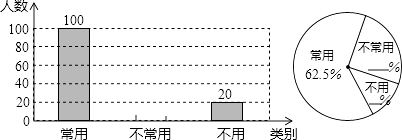
请根据上述统计图提供的信息,完成下列问题:
(1)这次抽查的样本容量是;
(2)请补全上述条形统计图和扇形统计图;
(3)若从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是多少?
参考答案:
【答案】
(1)160
(2)解:不常用计算器的人数为:160﹣100﹣20=40;
不常用计算器的百分比为:40÷160=25%,
不用计算器的百分比为:20÷160=12.5%.
条形统计图和扇形统计图补全如下:
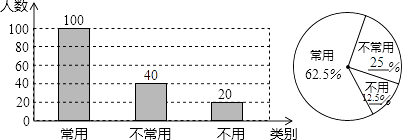
(3)解:∵“不常用”计算器的学生数为40,抽查的学生人数为160,
∴从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是: ![]() .
.
答:从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”的概率是 ![]()
【解析】解:(1)100÷62.5%=160.即这次抽查的样本容量是160.故答案为160;(1)根据条形图知道常用计算器的人数有100人,从扇形图知道常用计算器的占62.5%,从而可求出解;(2)用样本容量减去常用计算器的人数和不用计算器的人数求出不常用计算器的人数,再算出各部分的百分比补全条形图和扇形图;(3)学生恰好抽到“不常用”计算器的概率是“不常用”计算器的学生数除以抽查的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的顶点A、C分别在直线a、b上,且a∥b , ∠1=65°,则∠2的度数为
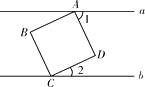
A.65°
B.55°
C.35°
D.25° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.

(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题为真命题的是
A.有两边及一角对应相等的两个三角形全等
B.方程x2+2x+3=0有两个不相等的实数根
C.面积之比为1∶2的两个相似三角形的周长之比是1∶4
D.顺次连接任意四边形各边中点得到的四边形是平行四边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】一般情况下
 不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得
不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得 成立的一对数a,b为“相伴数对”,记为(a,b).
成立的一对数a,b为“相伴数对”,记为(a,b).(1)若(1,b)是“相伴数对”,求b的值;
(2)若(m,n)是“相伴数对”,其中m≠0,求
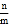 ;
;(3)若(m,n)是“相伴数对”,求代数式m﹣
 ﹣[4m﹣2(3n﹣1)]的值.
﹣[4m﹣2(3n﹣1)]的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种对正整数n的“F运算”:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为
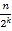 (其中k是使
(其中k是使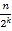 为奇数的正整数);并且运算重复进行.例如,取n=26,第3次“F运算”的结果是11.则:若n=449,则第449次“F运算”的结果是____.
为奇数的正整数);并且运算重复进行.例如,取n=26,第3次“F运算”的结果是11.则:若n=449,则第449次“F运算”的结果是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.

(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点C,若ACAB=12,求AC的长.
相关试题

