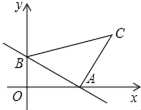
【题目】一次函数y=﹣![]() x+2的图象与x轴,y轴分别交于A、B两点,以AB为腰,作等腰Rt△ABC,则直线BC的解析式为( )
x+2的图象与x轴,y轴分别交于A、B两点,以AB为腰,作等腰Rt△ABC,则直线BC的解析式为( )
A. y=![]() x+2 B. y=﹣
x+2 B. y=﹣![]() x+2 C. y=﹣
x+2 C. y=﹣![]() x+2 D. y=
x+2 D. y=![]() x+2
x+2
参考答案:
【答案】D
【解析】
先根据一次函数的解析式求出A、B两点的坐标,再作CE⊥x轴于点E,由全等三角形的判定定理可得出△ABO≌△CAE,得出C点坐标,用待定系数法即可求出直线BC的解析式;
解:∵一次函数y=﹣![]() x+2中,
x+2中,
令x=0得:y=2;令y=0,解得x=5,
∴B的坐标是(0,2),A的坐标是(5,0).
如图,作CE⊥x轴于点E,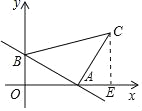
∵∠BAC=90°,
∴∠OAB+∠CAE=90°,
又∵∠CAE+∠ACE=90°,
∴∠ACE=∠BAO.
在△ABO与△CAE中,
![]()
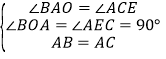 ,
,
∴△ABO≌△CAE(AAS),
∴OB=AE=2,OA=CE=5,
∴OE=OA+AE=2+5=7.
则C的坐标是(7,5).
设直线BC的解析式是y=kx+b,
根据题意得:![]() ,
,
解得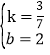 ,
,
∴直线BC的解析式是y=![]() x+2.
x+2.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图:∠1=∠2,∠3+∠4= 180°;确定直线a,c的位置关系,并说明理由;
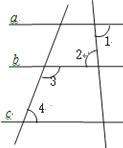
解:a c;
理由:∵∠1=∠2( ),
∴ a // ( );
∵ ∠3+∠4= 180°( ),
∴ c // ( );
∵ a // ,c // ,
∴ // ( );
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠EOF=60°,PA∥OF,PB∥OE,PC⊥OF于点C,求∠BPC的度数.
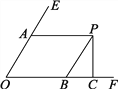
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地植物园从正门到侧门有一条小路,甲徒步从正门出发匀速走向侧门,乙与甲同时出发,骑自行车从侧门匀速前往正门到达正门后休息0.2小时,然后按原路原速匀速返回侧门,图中折线分别表示甲、乙到侧门的距离y(km)与出发时间x(h)之间的函数关系图象,根据图象信息解答下列问题:
(1)求甲到侧门的距离y与x之间的函数关系式;
(2)求甲、乙第一次相遇时到侧门的距离.
(3)求甲、乙第二次相遇的时间.
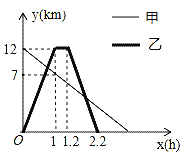
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB//CD,分别写出下列四个图形中,∠P与∠A、∠C的关系,请你从所得的四个关系中任选一个加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△AOB中,∠AOB为直角,A(﹣3,a)、B(3,b),a+b﹣12=0,则△AOB的面积为_____.
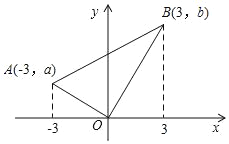
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,表示小王骑自行车和小李骑摩托车者沿相同的路线由甲地到乙地行驶过程的函数图象,两地相距80千米,请根据图象解决下列问题:
(1)哪一个人出发早?早多长时间?哪一个人早到达目的地?早多长时间?
(2)求出两个人在途中行驶的速度是多少?
(3)分别求出表示自行车和摩托车行驶过程的函数关系式.

相关试题

