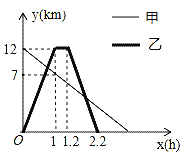
【题目】某地植物园从正门到侧门有一条小路,甲徒步从正门出发匀速走向侧门,乙与甲同时出发,骑自行车从侧门匀速前往正门到达正门后休息0.2小时,然后按原路原速匀速返回侧门,图中折线分别表示甲、乙到侧门的距离y(km)与出发时间x(h)之间的函数关系图象,根据图象信息解答下列问题:
(1)求甲到侧门的距离y与x之间的函数关系式;
(2)求甲、乙第一次相遇时到侧门的距离.
(3)求甲、乙第二次相遇的时间.
参考答案:
【答案】(1)y=﹣5x+12(2)![]() (3)
(3)![]()
【解析】
(1)根据函数图象可知点(0,12)和点(1,7)在甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数图象上,从而可以解答本题;
(2)根据函数图象可以分别求得甲乙刚开始两端对应的函数解析式,联立方程组即可求得甲、乙第一次相遇时到侧门的距离;
(3)根据函数图象可以得到在最后一段甲对应的函数解析式,联立方程组即可求得甲、乙第二次相遇的时间.
(1)设甲到侧门的距离y与x之间的函数关系式为y=kx+b(k≠0),
将(0,12),(1,7)代入y=kx+b,得:
![]() ,解得:
,解得:![]() ,
,
∴甲到侧门的距离y与x之间的函数关系式为y=﹣5x+12.
(2)设当0≤x≤1时,乙到侧门的距离y与x之间的函数关系式为y=ax(a≠0),
将(1,12)代入y=ax,得:12=a,
∴当0≤x≤1时,乙到侧门的距离y与x之间的函数关系式为y=12x.
联立两函数关系式成方程组,得:![]() ,
,
解得: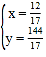 ,
,
∴甲、乙第一次相遇时到侧门的距离为![]() km.
km.
(3)设当1.2≤x≤2.2时,乙到侧门的距离y与x之间的函数关系式为y=mx+n(m≠0),
将(1.2,12),(2.2,0)代入y=mx+n,得:
![]() ,解得:
,解得:![]() ,
,
∴当1.2≤x≤2.2时,乙到侧门的距离y与x之间的函数关系式为y=﹣12x+26.4.
联立两函数关系式成方程组,得:![]() ,
,
解得: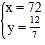 ,
,
∴甲、乙第二次相遇的时间为![]() h.
h.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(a,6)是第一象限内正比例函数y=3x的图象上的一点,AB⊥x轴,交直线OB于B点,三角形OAB的面积为5,求直线OB所对应的函数表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图:∠1=∠2,∠3+∠4= 180°;确定直线a,c的位置关系,并说明理由;
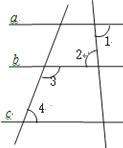
解:a c;
理由:∵∠1=∠2( ),
∴ a // ( );
∵ ∠3+∠4= 180°( ),
∴ c // ( );
∵ a // ,c // ,
∴ // ( );
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠EOF=60°,PA∥OF,PB∥OE,PC⊥OF于点C,求∠BPC的度数.
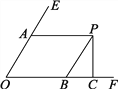
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=﹣
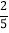 x+2的图象与x轴,y轴分别交于A、B两点,以AB为腰,作等腰Rt△ABC,则直线BC的解析式为( )
x+2的图象与x轴,y轴分别交于A、B两点,以AB为腰,作等腰Rt△ABC,则直线BC的解析式为( )
A. y=
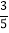 x+2 B. y=﹣
x+2 B. y=﹣ x+2 C. y=﹣
x+2 C. y=﹣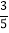 x+2 D. y=
x+2 D. y= x+2
x+2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB//CD,分别写出下列四个图形中,∠P与∠A、∠C的关系,请你从所得的四个关系中任选一个加以证明.

-
科目: 来源: 题型:
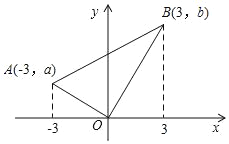
查看答案和解析>>【题目】如图,在Rt△AOB中,∠AOB为直角,A(﹣3,a)、B(3,b),a+b﹣12=0,则△AOB的面积为_____.
相关试题

