【题目】已知:如图:∠1=∠2,∠3+∠4= 180°;确定直线a,c的位置关系,并说明理由;
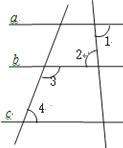
解:a c;
理由:∵∠1=∠2( ),
∴ a // ( );
∵ ∠3+∠4= 180°( ),
∴ c // ( );
∵ a // ,c // ,
∴ // ( );
参考答案:
【答案】答案见解析
【解析】试题分析:本题考查的是同学们对于平行线的判定的运用能力,内错角相等的两条直线平行;同旁内角互补的两条直线平行;平行于同一条直线的两条直线平行.
解:a // c;
理由:∵∠1=∠2( 已知 ),
∴ a // b ( 内错角相等,两直线平行 );
∵ ∠3+∠4= 180°( 已知 ),
∴ c // b ( 同旁内角互补, 两直线平行 );
∵ a // b ,c // b ,
∴ a // c ( 平行于同一条直线的两条直线平行 );
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,MN、EF分别表示两个互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的光线为CD,此时∠3=∠4.试判断AB与CD的位置关系,你是如何思考的?
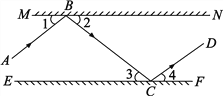
-
科目: 来源: 题型:
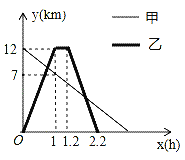
查看答案和解析>>【题目】某地植物园从正门到侧门有一条小路,甲徒步从正门出发匀速走向侧门,乙与甲同时出发,骑自行车从侧门匀速前往正门到达正门后休息0.2小时,然后按原路原速匀速返回侧门,图中折线分别表示甲、乙到侧门的距离y(km)与出发时间x(h)之间的函数关系图象,根据图象信息解答下列问题:
(1)求甲到侧门的距离y与x之间的函数关系式;
(2)求甲、乙第一次相遇时到侧门的距离.
(3)求甲、乙第二次相遇的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(a,6)是第一象限内正比例函数y=3x的图象上的一点,AB⊥x轴,交直线OB于B点,三角形OAB的面积为5,求直线OB所对应的函数表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠EOF=60°,PA∥OF,PB∥OE,PC⊥OF于点C,求∠BPC的度数.
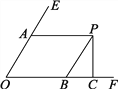
-
科目: 来源: 题型:
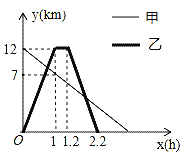
查看答案和解析>>【题目】某地植物园从正门到侧门有一条小路,甲徒步从正门出发匀速走向侧门,乙与甲同时出发,骑自行车从侧门匀速前往正门到达正门后休息0.2小时,然后按原路原速匀速返回侧门,图中折线分别表示甲、乙到侧门的距离y(km)与出发时间x(h)之间的函数关系图象,根据图象信息解答下列问题:
(1)求甲到侧门的距离y与x之间的函数关系式;
(2)求甲、乙第一次相遇时到侧门的距离.
(3)求甲、乙第二次相遇的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=﹣
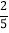 x+2的图象与x轴,y轴分别交于A、B两点,以AB为腰,作等腰Rt△ABC,则直线BC的解析式为( )
x+2的图象与x轴,y轴分别交于A、B两点,以AB为腰,作等腰Rt△ABC,则直线BC的解析式为( )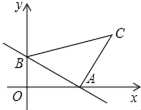
A. y=
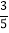 x+2 B. y=﹣
x+2 B. y=﹣ x+2 C. y=﹣
x+2 C. y=﹣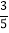 x+2 D. y=
x+2 D. y= x+2
x+2
相关试题

