【题目】如图,在⊙O的内接四边形ACDB中,AB为直径,AC:BC=1:2,点D为弧AB的中点,BE⊥CD垂足为E. 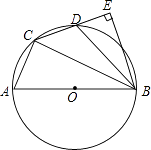
(1)求∠BCE的度数;
(2)求证:D为CE的中点;
(3)连接OE交BC于点F,若AB= ![]() ,求OE的长度.
,求OE的长度. 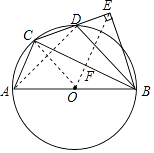
参考答案:
【答案】
(1)解:连接AD,

∵D为弧AB的中点,
∴AD=BD,
∵AB为直径,
∴∠ADB=90°,
∴∠DAB=∠DBA=45°,
∴∠DCB=∠DAB=45°
(2)解:证明:∵BE⊥CD,又∵∠ECB=45°,
∴∠CBE=45°,
∴CE=BE,
∵四边形ACDB是圆O的内接四边形,
∴∠A+∠BDC=180°,
又∵∠BDE+∠BDC=180°,
∴∠A=∠BD,
又∵∠ACB=∠BED=90°,
∴△ABC∽△DBE,
∴DE:AC=BE:BC,
∴DE:BE=AC:BC=1:2,
又∵CE=BE,
∴DE:CE=1:2,
∴D为CE的中点
(3)解:∵CO=BO,CE=BE,
∴OE垂直平分BC,
∴F为BC中点,
又∵O为AB中点,
∴OF为△ABC的中位线,
∴OF= ![]() AC,
AC,
∵∠BEC=90°,EF为中线,
∴EF= ![]() BC,
BC,
在Rt△ACB中,AC2+BC2=AB2,
∵AC:BC=1:2,AB= ![]() ,
,
∴AC= ![]() ,BC=2
,BC=2 ![]() ,
,
∴OE=OF+EF=1.5 ![]() .
.
【解析】(1)连接AD,由D为弧AB的中点,得到AD=BD,根据圆周角定理即可得到结论;(2)由已知条件得到∠CBE=45°,根据圆内接四边形的性质得到∠A=∠BD,根据相似三角形的性质得到DE:AC=BE:BC,即可得到结论.(3)连接CO,根据线段垂直平分线的判定定理得到OE垂直平分BC,由三角形的中位线到现在得到OF= ![]() AC,根据直角三角形的性质得到EF=
AC,根据直角三角形的性质得到EF= ![]() BC,由勾股定理即可得到结论.
BC,由勾股定理即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC=BC,点D在BC上,作∠ADF=∠B,DF交外角∠ACE的平分线CF于点F.

(1)求证:CF∥AB;
(2)若∠CAD=20°,求∠CFD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小河边有两个村庄A、B,要在河边建一自来水厂向A村与B村供水。
(1)若要使水厂到A、B村的距离相等,则应选择在哪建厂?
(2)若要使水厂到A、B村的水管最省料,应建在什么地方?

-
科目: 来源: 题型:
查看答案和解析>>【题目】操作与探究.
(1)分别画出图①中“
 ”和“
”和“ ”关于直线l的对称图形(画出示意图即可).
”关于直线l的对称图形(画出示意图即可).(2)图②中小冬和小亮上衣上印的字母分别是什么?
(3)把字母“
 ”和“
”和“ ”写在薄纸上,观察纸的背面,写出你看到的字母背影.
”写在薄纸上,观察纸的背面,写出你看到的字母背影.(4)小明站在五个学生的身后,这五个学生正向前方某人用手势示意一个五位数,从小明站的地方看(如图③所示),这个五位数是23456.请你判断出他们示意的真实五位数是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=a(x+2)(x﹣4)(a为常数,且a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣
 x+b与抛物线的另一交点为D,且点D的横坐标为﹣5.
x+b与抛物线的另一交点为D,且点D的横坐标为﹣5.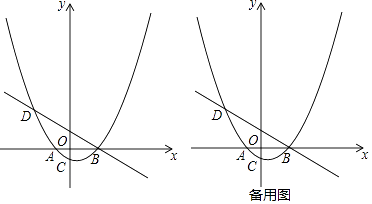
(1)求抛物线的函数表达式;
(2)P为直线BD下方的抛物线上的一点,连接PD、PB,求△PBD面积的最大值;
(3)设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一组自然数1,2,3…k,去掉其中一个数后剩下的数的平均数为16,则去掉的数是________.
相关试题

