【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

参考答案:
【答案】(1)利用SAS公式求证(2)![]()
【解析】
解:(1)①∵![]() 秒,
秒,
∴![]() 厘米,
厘米,
∵![]() 厘米,点
厘米,点![]() 为
为![]() 的中点,
的中点,
∴![]() 厘米.
厘米.
又∵![]() 厘米,
厘米,
∴![]() 厘米,
厘米,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
②∵![]() , ∴
, ∴![]() ,
,
又∵![]() ,
,![]() ,则
,则![]() ,
,
∴点![]() ,点
,点![]() 运动的时间
运动的时间![]() 秒,
秒,
∴![]() 厘米/秒.
厘米/秒.
(2)设经过![]() 秒后点
秒后点![]() 与点
与点![]() 第一次相遇,
第一次相遇,
由题意,得![]() ,
,
解得![]() 秒.
秒.
∴点![]() 共运动了
共运动了![]() 厘米.
厘米.
∵![]() ,
,
∴点![]() 、点
、点![]() 在
在![]() 边上相遇,
边上相遇,
∴经过![]() 秒点
秒点![]() 与点
与点![]() 第一次在边
第一次在边![]() 上相遇.
上相遇.
(1)①根据时间和速度分别求得两个三角形中的边的长,根据SAS判定两个三角形全等.
②根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点P运动的时间,再求得点Q的运动速度;
(2)根据题意结合图形分析发现:由于点Q的速度快,且在点P的前边,所以要想第一次相遇,则应该比点P多走三角形的两个边AB,AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,AB>AC,BE,CF都是△ABC的高线,P是BE上一点,且BP=AC,Q是CF延长线上一点,且CQ=AB,连结AP,AQ,QP.求证:
(1)AQ=PA.
(2)AP⊥AQ.

-
科目: 来源: 题型:
查看答案和解析>>【题目】数学家高斯在上学时曾经研究过这样一个问题,
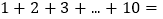 ?
?经过研究,这个问题的一般性结论是
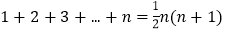 ,其中
,其中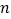 为正整数,现在我们来研究一个类似的问题:
为正整数,现在我们来研究一个类似的问题: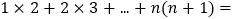 ?
?观察下面三个特殊的等式:


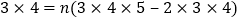
将这三个等式的两边相加,可以得到
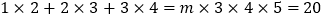 .
.读完这段材料,请你计算:
(1)
 ________;(直接写出结果)
________;(直接写出结果)(2)
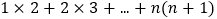 ;(写出计算过程)
;(写出计算过程)(3)
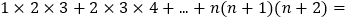 ________.
________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 度;
(2)设∠BAC=
 ,∠DCE=
,∠DCE=  .
.① 如图2,当点D在线段CB上,∠BAC≠90°时,请你探究
 与
与 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;② 如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时
 与
与 之间的数量关系(不需证明).
之间的数量关系(不需证明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )

A. 2
 B. 3
B. 3 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角△ABC中,∠BAC=90°,BC=6,过点C作CD⊥BC,CD=2,连接BD,过点C作CE⊥BD,垂足为E,连接AE,则AE长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,AB=5,在AB边上有一点P,过点P作PM⊥BC,垂足为M,过点M作MN⊥AC,垂足为N,过点N作NQ⊥AB,垂足为Q.当PQ=1时,BP=_____.
相关试题

