【题目】以下问题中的数据在美国的历史上都是真实的,试对此现象进行分析:
(1) 亚利桑那州历来是一个风景优美,气候宜人的地方,尤其有利于肺结核病人的疗养、康复.可是十九世纪有一位统计学家发现,在亚利桑那州死于肺结核的人数远较其他州多,患者比例普遍达到其他州的 ![]() 至
至 ![]() 倍.人们一度对这里优美的环境望而却步,给当地的旅游、疗养业造成了巨大的影响.
倍.人们一度对这里优美的环境望而却步,给当地的旅游、疗养业造成了巨大的影响.
(2) 上个世纪,某地的房产开发商曾对当时每户家庭人数进行过较大规模的调查,得到的结论是平均每户 ![]() 人.据此,在当年的住房设计中主要考虑了适宜
人.据此,在当年的住房设计中主要考虑了适宜 ![]() 人家庭居住的户型,结果造成了滞销,而适宜
人家庭居住的户型,结果造成了滞销,而适宜 ![]() 至
至 ![]() 人家庭居住的小户型和
人家庭居住的小户型和 ![]() 人以上的大户型却供不应求.
人以上的大户型却供不应求.
参考答案:
【答案】(1) 见解析; (2) 见解析.
【解析】试题分析:(1)只关注亚利桑那州死于肺结核的人数远较其他州多,不考虑其他方面,因此是片面的;
(2)平均每户3.6人并不表示大多数家庭规模为近4人,想想应该关注什么数最合适?
试题解析:(1) 由于亚利桑那州的气候、环境有利于肺结核病人的康复,所以必然会有大量外地患者前来疗养,患者比例、死亡人数的增加就不足为奇.要正确评价当地环境对肺结核患者的作用,应同时调查肺结核病人的治愈、好转率,当地居民中肺结核的发病率等.
(2) 平均每户 ![]() 人并不表示大多数家庭规模为近
人并不表示大多数家庭规模为近 ![]() 人.开发商在关注家庭人数平均数、众数的同时应对数据作全面分析,并注重对近期准备购房对象作调查.事实上,当地媒体事后公布的数据是全部家庭中,
人.开发商在关注家庭人数平均数、众数的同时应对数据作全面分析,并注重对近期准备购房对象作调查.事实上,当地媒体事后公布的数据是全部家庭中, ![]() 人家庭占
人家庭占 ![]() ,
, ![]() 人家庭占
人家庭占 ![]() ,
, ![]() 人以上家庭占
人以上家庭占 ![]() ;而两年内购买新房的家庭中
;而两年内购买新房的家庭中 ![]() 人家庭占
人家庭占 ![]() ,
, ![]() 人家庭占
人家庭占 ![]() ,
, ![]() 人以上家庭占
人以上家庭占 ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“爱我中华”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:甲:8,7,9,8,8;乙:7,9,6,9,9,则下列说法中错误的是( )
A. 甲得分的方差比乙得分的方差小B. 甲得分的众数是8,乙得分的众数是9
C. 甲、乙得分的平均数都是8D. 甲得分的中位数是9,乙得分的中位数是6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=3a2b-2ab2+abc,小明同学错将“2A-B”看成“2A+B”,算得结果为4a2b-3ab2+4abc.
(1)求出2A-B的结果;
(2)小强同学说(1)中的结果的大小与c的取值无关,正确吗?若a=
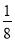 ,b=
,b=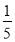 ,求(1)中式子的值.
,求(1)中式子的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图 ,在平行四边形 ABCD 中DAB 的平分线交CD 于点 E ,交 BC 的延长线于点G ,∠ABC的平分线交CD 于点 F ,交 AD 的延长线于点 H ,交 AG 与 BH 成交于点O ,连接 BE 。下列结论错误的是( )

A.BO OHB.DF CEC.DH CGD.AB AE
-
科目: 来源: 题型:
查看答案和解析>>【题目】一天课间,顽皮的小明同学拿着老师的等腰三角板玩,不小心掉到两根柱子之间,如图所示,这一幕恰巧被数学老师看见了,于是有了下面这道题.
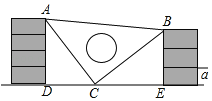
(1)求证:△ADC≌△CEB;
(2)如果每块砖的厚度a=10cm,请你帮小明求出三角板ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】八年 2 班组织了一次经典诵读比赛,甲乙两组各 10 人的比赛成绩如下表(10 分制):
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
(Ⅰ)甲组数据的中位数是 ,乙组数据的众数是 ;
(Ⅱ)计算乙组数据的平均数和方差;
(Ⅲ)已知甲组数据的方差是 1.4 分,则成绩较为整齐的是 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】九(1)班同学为了解 2011 年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.请解答以下问题:



(1) 把上面的频数分布表和频数分布直方图补充完整;
(2) 求月均用水量不超过
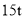 的家庭数占被调查家庭总数的百分比;
的家庭数占被调查家庭总数的百分比;(3) 若该小区有
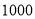 户家庭,根据调查数据估计,该小区月均用水量超过
户家庭,根据调查数据估计,该小区月均用水量超过 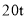 的家庭大约有多少户 ?
的家庭大约有多少户 ?
相关试题

