【题目】在“爱我中华”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:甲:8,7,9,8,8;乙:7,9,6,9,9,则下列说法中错误的是( )
A. 甲得分的方差比乙得分的方差小B. 甲得分的众数是8,乙得分的众数是9
C. 甲、乙得分的平均数都是8D. 甲得分的中位数是9,乙得分的中位数是6
参考答案:
【答案】D
【解析】
分别求出甲、乙的平均数、方差、众数、中位数即可逐一判断.
解:甲得分的平均数为:(8+7+9+8+8)÷5=8,乙得分的平均数为:(7+9+6+9+9)÷5=8;
甲得分的方差为:![]() ×[(8﹣8)2+(7﹣8)2+(9﹣8)2+(8﹣8)2+(8﹣8)2]=
×[(8﹣8)2+(7﹣8)2+(9﹣8)2+(8﹣8)2+(8﹣8)2]=![]() ×2=0.4,
×2=0.4,
乙得分的方差为:![]() ×[(7﹣8)2+(9﹣8)2+(6﹣8)2+(9﹣8)2+(9﹣8)2]=
×[(7﹣8)2+(9﹣8)2+(6﹣8)2+(9﹣8)2+(9﹣8)2]=![]() ×8=1.6,
×8=1.6,
故A、C都正确;
甲得分次数最多是8分,即众数为8分,乙得分最多的是9分,即众数为9分,故B正确;
C、∵甲得分从小到大排列为:7、8、8、8、9,∴甲的中位数是8分;
∵乙得分从小到大排列为:6、7、9、9、9,∴乙的中位数是9分;故D错误;
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A、B两个旅游点从2010年至2014年“五、一”的旅游人数变化情况分别用实线和虚线表示.根据图中所示解答以下问题:

(1)B旅游点的旅游人数相对上一年,增长最快的是哪一年?
(2)求A、B两个旅游点从2010到2014年旅游人数的平均数和方差,并从平均数和方差的角度,用一句话对这两个旅游点的情况进行评价.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点D为△ABC边BC的延长线上一点.

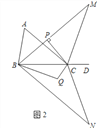
(1)若∠A∶∠ABC=3∶4,∠ACD=140°,求∠A的度数;
(2)若∠ABC的角平分线与∠ACD的角平分线交于点M,过点C作CP⊥BM于点P.
求证:
 ;
;(3)在(2)的条件下,将△MBC以直线BC为对称轴翻折得到△NBC,∠NBC的角平分线与∠NCB的角平分线交于点Q(如图2),试探究∠BQC与∠A有怎样的数量关系,请写出你的猜想并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级所有女生的身高统计数据如下表,请回答下列问题:
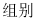
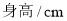
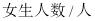
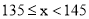
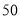
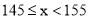
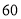
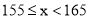
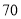
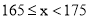
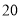
(1) 这个学校八年级共有多少女生?
(2) 身高在
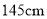 到
到  的女生有多少人?
的女生有多少人?(3) 一女生的身高恰好为
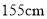 ,哪一组包含这个身高?这一组出现的频数、频率各是多少?
,哪一组包含这个身高?这一组出现的频数、频率各是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=3a2b-2ab2+abc,小明同学错将“2A-B”看成“2A+B”,算得结果为4a2b-3ab2+4abc.
(1)求出2A-B的结果;
(2)小强同学说(1)中的结果的大小与c的取值无关,正确吗?若a=
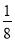 ,b=
,b=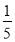 ,求(1)中式子的值.
,求(1)中式子的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图 ,在平行四边形 ABCD 中DAB 的平分线交CD 于点 E ,交 BC 的延长线于点G ,∠ABC的平分线交CD 于点 F ,交 AD 的延长线于点 H ,交 AG 与 BH 成交于点O ,连接 BE 。下列结论错误的是( )

A.BO OHB.DF CEC.DH CGD.AB AE
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下问题中的数据在美国的历史上都是真实的,试对此现象进行分析:
(1) 亚利桑那州历来是一个风景优美,气候宜人的地方,尤其有利于肺结核病人的疗养、康复.可是十九世纪有一位统计学家发现,在亚利桑那州死于肺结核的人数远较其他州多,患者比例普遍达到其他州的
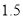 至
至  倍.人们一度对这里优美的环境望而却步,给当地的旅游、疗养业造成了巨大的影响.
倍.人们一度对这里优美的环境望而却步,给当地的旅游、疗养业造成了巨大的影响.(2) 上个世纪,某地的房产开发商曾对当时每户家庭人数进行过较大规模的调查,得到的结论是平均每户
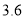 人.据此,在当年的住房设计中主要考虑了适宜
人.据此,在当年的住房设计中主要考虑了适宜 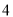 人家庭居住的户型,结果造成了滞销,而适宜
人家庭居住的户型,结果造成了滞销,而适宜 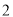 至
至  人家庭居住的小户型和
人家庭居住的小户型和  人以上的大户型却供不应求.
人以上的大户型却供不应求.
相关试题

