【题目】如图,已知直线y=-x+2与x轴、y轴分别交于点A和点B,另一直线y=kx+b(k≠0)经过点C(1,0),且把△AOB分成两部分.
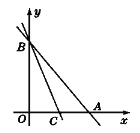
(1)若△AOB被分成的两部分面积相等,求k和b的值;
(2)若△AOB被分成的两部分面积比为1∶5,求k和b的值.
参考答案:
【答案】(1)b=2,k=-2(2)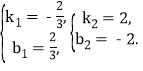
【解析】
(1)△AOB被分成的两部分面积相等,那么被分成的两部分都应该是三角形AOB的面积的一半,那么直线y=kx+b(k≠0)必过B点,因此根据B,C两点的函数关系式可得出,直线的函数式.
(2)若△AOB被分成的两部分面积比为1:5,那么被分成的两部分中小三角形的面积就应该是大三角形面积的![]() ,已知了直线过C点,则小三角形的底边是大三角形的OA边的一半,故小三角形的高应该是OB的
,已知了直线过C点,则小三角形的底边是大三角形的OA边的一半,故小三角形的高应该是OB的![]() ,即直线经过的这点的纵坐标应该是
,即直线经过的这点的纵坐标应该是![]() .那么这点应该在y轴和AB上,可分这两种情况进行计算,运用待定系数法求函数的解析式.
.那么这点应该在y轴和AB上,可分这两种情况进行计算,运用待定系数法求函数的解析式.
(1)由题意知:直线y=kx+b(k≠0)必过C点,
∵C是OA的中点,
∴直线y=kx+b一定经过点B,C,如图(1)所示,
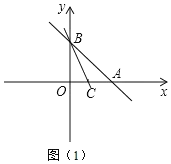
把B,C的坐标代入可得:
∴![]() ,
,
解得![]() ;
;
(2)∵S△AOB=![]() ×2×2=2,
×2×2=2,
∵△AOB被分成的两部分面积比为1:5,那么直线y=kx+b(k≠0)与y轴或AB交点的纵坐标就应该是:2×2×![]() =
=![]() ,
,
①当y=kx+b(k≠0)与直线y=x+2相交时,交点为D,如图(2)所示,
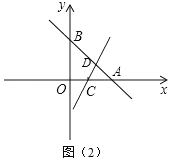
当y=![]() 时,直线y=x+2与y=kx+b(k≠0)的交点D的横坐标就应该是x+2=
时,直线y=x+2与y=kx+b(k≠0)的交点D的横坐标就应该是x+2=![]() ,
,
∴x=![]() ,
,
即交点D的坐标为(![]() ,
,![]() ),
),
又根据C点的坐标为(1,0),可得:

∴![]() ,
,
②当y=kx+b(k≠0)与y轴相交时,交点为E,如图(3)所示,
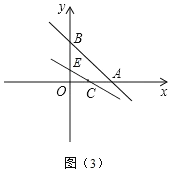
∴交点E的坐标就应该是(0,![]() ),又有C点的坐标(1,0
),又有C点的坐标(1,0
 ,
,
∴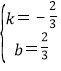
因此:k=2,b=2或k=![]() ,b=
,b=![]() .
.
-
科目: 来源: 题型:
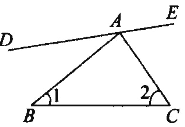
查看答案和解析>>【题目】如图,∠1和哪些角是内错角?∠1和哪些角是同旁内角?∠2和哪些角是内错角?∠2和哪些角是同旁内角?它们分别是由哪两条直线被哪一条线截成的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】找出图中所有的同位角、内错角、同旁内角.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(图象信息题)已知一次函数y=2x-1的图象如图所示,
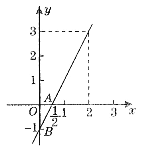
请根据图象解决下列问题:
(1)写出一次函数的图象与x轴y轴的交点坐标;
(2)写出方程2x-1=3的解;
(3)分别写出不等式2x-1>-1,2x-1≥0,2x-1<3的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
①△BO′A可以由△BOC绕点B逆时针旋转60°得到;
②点O与O′的距离为4;
③四边形AO BO′的面积为6+3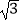
④∠AOB=150°;
⑤S△AOC+S△AOB=6+ .
.
其中正确的结论是( )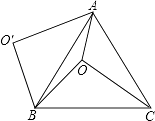
A.②③④⑤
B.①③④⑤
C.①②③⑤
D.①②④⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆警车在高速公路的A处加满油,以每小时60千米的速度匀速行驶.已知警车一次加满油后,油箱内的余油量y(升)与行驶时间x(小时)的函数关系的图象如图所示的直线l上的一部分.
(1)求直线l的函数关系式;
(2)如果警车要回到A处,且要求警车中的余油量不能少于10升,那么警车可以行驶到离A处的最远距离是多少?
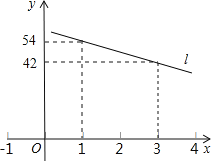
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=
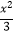 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 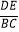 = .
= . 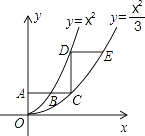
相关试题

