【题目】我县某包装生产企业承接了一批礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是![]() 的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下
的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下![]() 型与
型与![]() 型两种板材.如图所示,(单位:
型两种板材.如图所示,(单位:![]() )
)

(1)列出方程(组),求出图甲中![]() 与
与![]() 的值.
的值.
(2)在试生产阶段,若将![]() 张标准板材用裁法一裁剪,
张标准板材用裁法一裁剪,![]() 张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成如图的竖式与横式两种无盖礼品盒.
张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成如图的竖式与横式两种无盖礼品盒.
①两种裁法共产生A型板材 张,B型板材 张;
②设做成的竖式无盖礼品盒![]() 个,横式无盖礼品盒的
个,横式无盖礼品盒的![]() 个,根据题意完成表格:
个,根据题意完成表格:
礼品盒板 材 | 竖式无盖(个) | 横式无盖(个) |
|
| |
A型(张) |
|
|
B型(张) |
|

③做成的竖式和横式两种无盖礼品盒总数最多是 个;
此时,横式无盖礼品盒可以做 个(在横线上直接写出答案,无需书写过程)
参考答案:
【答案】(1)a=60,b=40(2)① 64,38 ② 2y③ 20;16或17或18
【解析】
(1)由图示列出关于a、b的二元一次方程组求解;
(2)根据已知和图示计算出两种裁法共产生A型板材和B型板材的张数,同样由图示完成表格,并完成计算.
(1)由题意得:![]() ,解得:
,解得:![]() .
.
答:图甲中a与b的值分别为:60、40.
(2)①由图示裁法一产生A型板材为:2×30=60,裁法二产生A型板材为:1×4=4,所以两种裁法共产生A型板材
为60+4=64(张),由图示裁法一产生B型板材为:1×30=30,裁法二产生A型板材为,2×4=8,所以两种裁法共产生B型板材
为30+8=38(张).
故答案为:64,38.
②由已知和图示得:横式无盖礼品盒的y个,每个礼品盒用2张B型板材,所以用B型板材2y张.
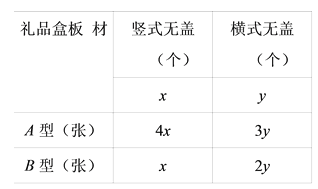
③由上表可知横式无盖款式共5y个面,用A型3y张,则B型需要2y张.
则做两款盒子共需要A型4x+3y张,B型x+2y张.
则4x+3y≤64;x+2y≤38.两式相加得5x+5y≤102.
则x+y≤20.4.所以最多做20个.
两式相减得3x+y≤26.则2x≤5.6,解得x≤2.8.则y≤18.
则横式可做16,17或18个.
故答案为:20,16或17或18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=4,CD=5。把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图2),此时AB与CD1交于点O,则线段AD1的长度为。

-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b图象经过点(1,3)和(4,6)
①试求
 与
与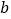 ;
;
②画出这个一次函数图象;
③这个一次函数与y轴交点坐标是( )
④当x 时,y<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着市民环保意识的增强,节庆期间烟花爆竹销售量逐年下降.某市2012年销售烟花爆竹20万箱,到2014年烟花爆竹销售量为9.8万箱.求该市2012年到2014年烟花爆竹年销售量的平均下降率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A (3,2)、B(1,3)。△AOB绕点O 逆时针旋转90°后得到△A1OB1.

(1)画出旋转后的图形;
(2)求线段OB在旋转过程中所扫过的图形面积(写过程)。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动,设运动时间为x(秒),△PBQ的面只为y(cm2).

(1)求y关于x的函数关系式,并写出x的取值范围.
(2)求△PBQ的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某农场有A、B两种型号的收割机共20台,每台A型收割机每天可收大麦100亩或者小麦80亩,每台B型收割机每天可收大麦80亩或者小麦60亩,该农场现有19 000亩大麦和11 500亩小麦先后等待收割.先安排这20台收割机全部收割大麦,并且恰好10天时间全部收完.
(1)问A、B两种型号的收割机各多少台?
(2)由于气候影响,要求通过加班方式使每台收割机每天多完成10%的收割量,问这20台收割机能否在一周时间内完成全部小麦收割任务?
相关试题

