【题目】如图,把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=4,CD=5。把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图2),此时AB与CD1交于点O,则线段AD1的长度为。 
参考答案:
【答案】解:由题意易知:∠CAB=45°,∠ACD=30°.
若旋转角度为15°,则∠ACO=30°+15°=45°.
∴∠AOC=180°-∠ACO-∠CAO=90°.
在等腰Rt△ABC中,AB=4,则AC=BC=2![]() .
.
同理可求得:AO=OC=2.
在Rt△AOD1中,OA=2,OD1=CD1-OC=3,
由勾股定理得: AD1=![]() .
.
【解析】抓住已知把一副三角板如图(1)放置,可知∠CAB=45°,∠ACD=30°.根据旋转的性质求出∠ACO的度数,利用勾股定理,可求出AC、AO、OC的长,再求出OD1的长,在Rt△AOD1中,根据勾股定理即可求出结果。
【考点精析】根据题目的已知条件,利用勾股定理的概念和旋转的性质的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,若
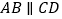 ,将点
,将点 在
在 内部,∠
内部,∠ ,∠
,∠ ,∠
,∠ 满足的数量关系是 ,并说明理由.
满足的数量关系是 ,并说明理由.(2)在如图1中,将直线
 绕点
绕点 逆时针方向旋转一定角度交直线
逆时针方向旋转一定角度交直线 于点
于点 ,如图2,利用(1)中的结论(可以直接套用),求∠
,如图2,利用(1)中的结论(可以直接套用),求∠ ﹑∠
﹑∠ ﹑∠
﹑∠ ﹑∠
﹑∠ 之间有何数量关系?
之间有何数量关系?
(3)科技活动课上,雨轩同学制作了一个图(3)的“飞旋镖”,经测量发现∠
 =
= °,∠
°,∠ =
= °,则∠
°,则∠ 与∠
与∠ 的数量关系是 .
的数量关系是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程(k-1)x2+2x-2=0有两个不相等的实数根,则k的取值范围是( )
A.k>
B.k≥
C.k> 且k≠1
且k≠1
D.k≥ 且k≠1
且k≠1 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图像如图所示,则①abc;②b2-4ac;③2a+b;④a+b+c这四个式子中,值为负数的有个( )

A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b图象经过点(1,3)和(4,6)
①试求
 与
与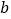 ;
;
②画出这个一次函数图象;
③这个一次函数与y轴交点坐标是( )
④当x 时,y<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着市民环保意识的增强,节庆期间烟花爆竹销售量逐年下降.某市2012年销售烟花爆竹20万箱,到2014年烟花爆竹销售量为9.8万箱.求该市2012年到2014年烟花爆竹年销售量的平均下降率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我县某包装生产企业承接了一批礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是
 的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下
的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下 型与
型与 型两种板材.如图所示,(单位:
型两种板材.如图所示,(单位: )
)
(1)列出方程(组),求出图甲中
 与
与 的值.
的值.(2)在试生产阶段,若将
 张标准板材用裁法一裁剪,
张标准板材用裁法一裁剪, 张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成如图的竖式与横式两种无盖礼品盒.
张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成如图的竖式与横式两种无盖礼品盒.①两种裁法共产生A型板材 张,B型板材 张;
②设做成的竖式无盖礼品盒
 个,横式无盖礼品盒的
个,横式无盖礼品盒的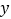 个,根据题意完成表格:
个,根据题意完成表格:礼品盒板 材
竖式无盖(个)
横式无盖(个)

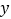
A型(张)


B型(张)


③做成的竖式和横式两种无盖礼品盒总数最多是 个;
此时,横式无盖礼品盒可以做 个(在横线上直接写出答案,无需书写过程)
相关试题

