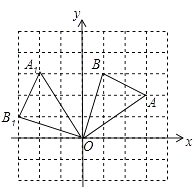
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A (3,2)、B(1,3)。△AOB绕点O 逆时针旋转90°后得到△A1OB1.
(1)画出旋转后的图形;
(2)求线段OB在旋转过程中所扫过的图形面积(写过程)。
参考答案:
【答案】
(1)解:如图所示,则 ![]() 为所求作的图形;
为所求作的图形;
(2)解:点B扫过的图形为扇形 ![]() ,∵旋转角为90°,∴
,∵旋转角为90°,∴ ![]() =90°,∵点B(1,3),∴
=90°,∵点B(1,3),∴ ![]() ,∴
,∴ ![]() =
= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)根据A 、B两点坐标,确定x轴和y轴,再将△AOB绕点O 逆时针旋转90°后得到△A1OB1,画出旋转后的图形。
(2)线段OB在旋转过程中所扫过的图形是以O为圆心,OB为半径的扇形,可知此扇形的圆心角为90°,再根据点B的坐标求出半径OB的长,即可求出此扇形的面积。
【考点精析】根据题目的已知条件,利用勾股定理的概念和扇形面积计算公式的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b图象经过点(1,3)和(4,6)
①试求
 与
与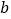 ;
;
②画出这个一次函数图象;
③这个一次函数与y轴交点坐标是( )
④当x 时,y<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着市民环保意识的增强,节庆期间烟花爆竹销售量逐年下降.某市2012年销售烟花爆竹20万箱,到2014年烟花爆竹销售量为9.8万箱.求该市2012年到2014年烟花爆竹年销售量的平均下降率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我县某包装生产企业承接了一批礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是
 的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下
的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下 型与
型与 型两种板材.如图所示,(单位:
型两种板材.如图所示,(单位: )
)
(1)列出方程(组),求出图甲中
 与
与 的值.
的值.(2)在试生产阶段,若将
 张标准板材用裁法一裁剪,
张标准板材用裁法一裁剪, 张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成如图的竖式与横式两种无盖礼品盒.
张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成如图的竖式与横式两种无盖礼品盒.①两种裁法共产生A型板材 张,B型板材 张;
②设做成的竖式无盖礼品盒
 个,横式无盖礼品盒的
个,横式无盖礼品盒的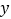 个,根据题意完成表格:
个,根据题意完成表格:礼品盒板 材
竖式无盖(个)
横式无盖(个)

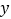
A型(张)


B型(张)


③做成的竖式和横式两种无盖礼品盒总数最多是 个;
此时,横式无盖礼品盒可以做 个(在横线上直接写出答案,无需书写过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动,设运动时间为x(秒),△PBQ的面只为y(cm2).

(1)求y关于x的函数关系式,并写出x的取值范围.
(2)求△PBQ的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某农场有A、B两种型号的收割机共20台,每台A型收割机每天可收大麦100亩或者小麦80亩,每台B型收割机每天可收大麦80亩或者小麦60亩,该农场现有19 000亩大麦和11 500亩小麦先后等待收割.先安排这20台收割机全部收割大麦,并且恰好10天时间全部收完.
(1)问A、B两种型号的收割机各多少台?
(2)由于气候影响,要求通过加班方式使每台收割机每天多完成10%的收割量,问这20台收割机能否在一周时间内完成全部小麦收割任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】西安市在创建文明城区的活动中,有两个长度相等的彩色砖道铺设任务,分别交给甲、乙两个施工队同时进行施工,如图是反映所铺设的彩色砖道的长度y(米)与施工时间x(小时)之间关系的部分图象,请解答下列问题:
(1)求乙队在0≤x≤6的时段内y与x的函数关系式.
(2)如果甲队施工速度不变,乙队在施工6小时后,施工速度增加到12米/小时,结果两队同时完成了任务,求甲队从开始施工到完成所铺设的彩色砖道的长度为多少米?

相关试题

