【题目】在平面直角坐标系中,将一个点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫做这个点的“互换点”,如(-3,5)与(5,-3)是一对“互换点”。
(1)任意一对“互换点”________(填“都能”或“都不能”)在一个反比例函数的图象上;
(2)M、N是一对“互换点”,若点M的坐标为(2,-5),求直线MN的表达式;
(3)在抛物线![]() 的图象上有一对“互换点”A、B,其中点A在反比例函数
的图象上有一对“互换点”A、B,其中点A在反比例函数![]() 的图象上,直线AB经过点P(
的图象上,直线AB经过点P(![]() ,
,![]() ),求此抛物线的表达式.
),求此抛物线的表达式.
参考答案:
【答案】(1)不一定;(2)y=-x-3;(3)![]() .
.
【解析】
(1)设这一对“互换点”的坐标为(a,b)和(b,a).①当ab=0时,它们不可能在反比例函数的图象上,②当ab≠0时,由b=![]() 可得a=
可得a=![]() ,于是得到结论;
,于是得到结论;
(2)把M(2,-5),N(-5,2)代入y=cx+d,即可得到结论;
(3)设点A(p,q),则q=![]() ,由直线AB经过点P(
,由直线AB经过点P(![]() ,
,![]() ),得到p+q=1,得到q=-1或q=2,将这一对“互换点”代入y=x2+bx+c得,于是得到结论.
),得到p+q=1,得到q=-1或q=2,将这一对“互换点”代入y=x2+bx+c得,于是得到结论.
(1)不一定,
设这一对“互换点”的坐标为(a,b)和(b,a).
①当ab=0时,它们不可能在反比例函数的图象上,
②当ab≠0时,由b=![]() 可得a=
可得a=![]() ,即(a,b)和(b,a)都在反比例函数y=
,即(a,b)和(b,a)都在反比例函数y=![]() (k≠0)的图象上;
(k≠0)的图象上;
(2)由M(2,-5)得N(-5,2),设直线MN的表达式为y=cx+d(c≠0).
则有![]()
解得,![]() ,
,
∴直线MN的表达式为y=-x-3;
(3)设点A(p,q),则q=![]() ,
,
∵直线AB经过点P(![]() ,
,![]() ),由(2)得
),由(2)得![]() =
=![]() +p+q,
+p+q,
∴p+q=1,
∴p![]() =1,
=1,
解并检验得:p=2或p=-1,
∴q=-1或q=2,
∴这一对“互换点”是(2,-1)和(-1,2),
将这一对“互换点”代入y=x2+bx+c得,
∴![]() ,解得
,解得![]() ,
,
∴此抛物线的表达式为y=x2-2x-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在
 中,
中, ,
, ,
, 分别是
分别是 的高线和角平分线.
的高线和角平分线.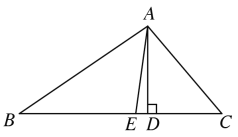
(1)若
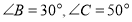 ,求
,求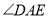 的度数;
的度数;(2)试写出
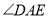 与
与 有何关系?(不必证明)
有何关系?(不必证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】某“数学兴趣小组”根据学习函数的经验,对函数
 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:(1)自变量x的取值范围是全体实数,x与y的几组对应数值如下表:
x
…
-3
-

-2
-1
0
1
2

3
…
y
…
-2
-
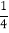
m
2
1
2
1
-
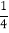
-2
…
其中m=____________;
(2)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;

(3)根据函数图象
①写出该函数的一条性质_______________;
②直线
 经过点(-l,2),若关于x的方程
经过点(-l,2),若关于x的方程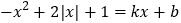 有4个互不相等的实数根,则b的取值范围是__________________.
有4个互不相等的实数根,则b的取值范围是__________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在等腰直角三角形
 中,
中,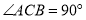 ,
,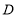 为
为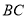 的中点,且
的中点,且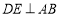 ,垂足为点
,垂足为点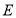 ,过点
,过点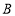 作
作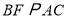 交
交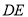 的延长线于点
的延长线于点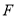 ,联结
,联结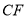 .
.(1)求证:
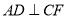 ;
;(2)连接
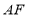 ,试判断
,试判断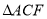 的形状,并说明理由.
的形状,并说明理由.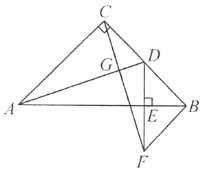
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠C=90°,AC=BC,点D在射线BC上(不与点B、C重合),连接AD,将AD绕点D顺时针旋转90°得到DE,连接BE.
(1)如图1,点D在BC边上.
①依题意补全图1;
②作DF⊥BC交AB于点F,若AC=8,DF=3,求BE的长;
(2)如图2,点D在BC边的延长线上,用等式表示线段AB、BD、BE之间的数量关系(直接写出结论).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出如下定义:
若b′=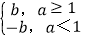 ,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(-2,5)的限变点的坐标是(-2,-5).
,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(-2,5)的限变点的坐标是(-2,-5).
(1)①点(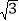 ,1)的限变点的坐标是 ;
,1)的限变点的坐标是 ;
②在点A(-2,-1),B(-1,2)中有一个点是函数y=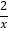 图象上某一个点的限变点,这个点是 ;(填“A”或“B”)
图象上某一个点的限变点,这个点是 ;(填“A”或“B”)
(2)若点P在函数y=-x+3(-2≤x≤k,k>-2)的图象上,其限变点Q的纵坐标b′的取值范围是-5≤b′≤2,求k的取值范围 ;
(3)若点P在关于x的二次函数y=x2-2tx+t2+t的图象上,其限变点Q的纵坐标b′的取值范围是b′≥m或b′<n,其中m>n.令s=m-n,求s关于t的函数解析式及s的取值范围 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了进一步开展“阳光体育”活动,购买了一批乒乓球拍和羽毛球拍,已知一副羽毛球拍比一副乒乓球拍费贵20元,购买羽毛球拍的费用比购买乒乓球拍的2000元要多,多出部分能购买25副乒乓球拍.
(1)若每副乒乓球拍的价格为x元,请你用含x的代数式表示该校购买这批乒乓球拍和羽毛球拍的总费用.
(2)若购买的两种球拍数一样,求x.
相关试题

