搜索
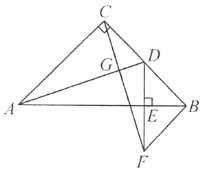
【题目】已知：如图，在等腰直角三角形
中，
，
为
的中点，且
，垂足为点
，过点
作
交
的延长线于点
，联结
.
（1）求证：
；
（2）连接
，试判断
的形状，并说明理由.
参考答案：
【答案】（1）见解析；（2）
是等腰三角形，理由见解析.
【解析】
（1）由
和
证明△DBF=等腰直角三角形，再证明
，得
，从而证明
；
（2）证明
，可得
，再由（1）知
，从而证明
，即可说明△ACF的性质.
（1）证明：
，，
，
∵
，
∴∠FEB=90°，
∴∠BFE=45°，
∴△DBF=等腰直角三角形，
∴DB=BF，
∵
为
的中点，
∴DC=BD，
∴DC=FB，
在△ACD和△CBF中
，
，
，
；
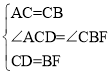
（2）连接
，
由（1）知△DBF等腰直角三角形，
，
∴DE=FE，
在△ADE和△AFE中
，
，
由（1）知，
，
，
是等腰三角形.
-
科目： 来源： 题型：
查看答案和解析>>【题目】中踏集团销售某种商品，每件进价为10元。在销售过程中发现，平均每天的销售量y（件）与销售价x（元／件）（不低于进价）之间的关系可近似的看做一次函数：
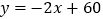；（1）求中踏集团平均每天销售这种商品的利润w（元）与销售价x之间的函数关系式；
（2）当这种商品的销售价为多少元时，可以获得最大利润，最大利润是多少?
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，在
中，
，
，
分别是的高线和角平分线．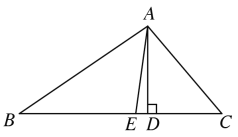
（1）若
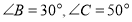，求
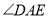的度数；（2）试写出
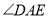与
有何关系？（不必证明） -
科目： 来源： 题型：
查看答案和解析>>【题目】某“数学兴趣小组”根据学习函数的经验，对函数
的图象和性质进行了探究，探究过程如下，请补充完整：（1）自变量x的取值范围是全体实数，x与y的几组对应数值如下表：
x
…
－3
－
－2
－1
0
1
2
3
…
y
…
－2
－
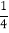
m
2
1
2
1
－
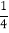
－2
…
其中m=____________；
（2）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
（3）根据函数图象
①写出该函数的一条性质_______________；
②直线
经过点（－l，2），若关于x的方程
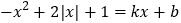有4个互不相等的实数根，则b的取值范围是__________________. -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，将一个点（横坐标与纵坐标不相等）的横坐标与纵坐标互换后得到的点叫做这个点的“互换点”，如（－3，5）与（5，－3）是一对“互换点”。
（1）任意一对“互换点”________（填“都能”或“都不能”）在一个反比例函数的图象上；
（2）M、N是一对“互换点”，若点M的坐标为（2，－5），求直线MN的表达式；
（3）在抛物线
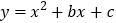的图象上有一对“互换点”A、B，其中点A在反比例函数
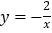的图象上，直线AB经过点P（
，），求此抛物线的表达式. -
科目： 来源： 题型：
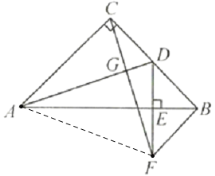
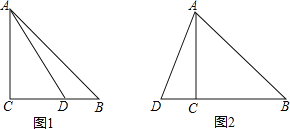
查看答案和解析>>【题目】在△ABC中，∠C=90°，AC=BC，点D在射线BC上（不与点B、C重合），连接AD，将AD绕点D顺时针旋转90°得到DE，连接BE．
（1）如图1，点D在BC边上．
①依题意补全图1；
②作DF⊥BC交AB于点F，若AC=8，DF=3，求BE的长；
（2）如图2，点D在BC边的延长线上，用等式表示线段AB、BD、BE之间的数量关系（直接写出结论）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，对于点P（a，b）和点Q（a，b′），给出如下定义：
若b′=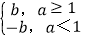
，则称点Q为点P的限变点．例如：点（2，3）的限变点的坐标是（2，3），点（-2，5）的限变点的坐标是（-2，-5）．
（1）①点(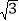
，1)的限变点的坐标是 ；
②在点A（-2，-1），B（-1，2）中有一个点是函数y＝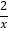
图象上某一个点的限变点，这个点是 ；（填“A”或“B”）
（2）若点P在函数y=-x+3（-2≤x≤k，k＞-2）的图象上，其限变点Q的纵坐标b′的取值范围是-5≤b′≤2，求k的取值范围 ；
（3）若点P在关于x的二次函数y=x2-2tx+t2+t的图象上，其限变点Q的纵坐标b′的取值范围是b′≥m或b′＜n，其中m＞n．令s=m-n，求s关于t的函数解析式及s的取值范围 ．
相关试题
