搜索
【题目】某校为了进一步开展“阳光体育”活动，购买了一批乒乓球拍和羽毛球拍，已知一副羽毛球拍比一副乒乓球拍费贵20元，购买羽毛球拍的费用比购买乒乓球拍的2000元要多，多出部分能购买25副乒乓球拍．
（1）若每副乒乓球拍的价格为x元,请你用含x的代数式表示该校购买这批乒乓球拍和羽毛球拍的总费用．
（2）若购买的两种球拍数一样，求x．
参考答案：
【答案】（1）
（元）（2）40元
【解析】
（1）根据该校购买这批乒乓球拍和羽毛球拍的总费用为“购买乒乓球拍的费用＋购买羽毛球拍的费用”列式即可．
（2）方程的应用解题关键是找出等量关系，列出方程求解．本题等量关系为：“购买的两种球拍数一样”．
解：（1）∵每副乒乓球拍的价格为x元，一副羽毛球拍比一副乒乓球拍费贵20元，
∴每副羽毛球拍为
元．
∵购买乒乓球拍的费用为2000元，购买羽毛球拍的费用比购买乒乓球拍的费用多25副乒乓球拍的费用，
∴羽毛球拍的费用为
元．
∴该校购买这批乒乓球拍和羽毛球拍的总费用为（元）．
（2）根据题意，得
，
解得
．
经检验，都是原方程的根，但
，∴
．
∴每副乒乓球拍的价格为x为40元．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，将一个点（横坐标与纵坐标不相等）的横坐标与纵坐标互换后得到的点叫做这个点的“互换点”，如（－3，5）与（5，－3）是一对“互换点”。
（1）任意一对“互换点”________（填“都能”或“都不能”）在一个反比例函数的图象上；
（2）M、N是一对“互换点”，若点M的坐标为（2，－5），求直线MN的表达式；
（3）在抛物线
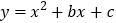的图象上有一对“互换点”A、B，其中点A在反比例函数
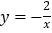的图象上，直线AB经过点P（
，），求此抛物线的表达式. -
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠C=90°，AC=BC，点D在射线BC上（不与点B、C重合），连接AD，将AD绕点D顺时针旋转90°得到DE，连接BE．
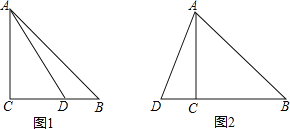
（1）如图1，点D在BC边上．
①依题意补全图1；
②作DF⊥BC交AB于点F，若AC=8，DF=3，求BE的长；
（2）如图2，点D在BC边的延长线上，用等式表示线段AB、BD、BE之间的数量关系（直接写出结论）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，对于点P（a，b）和点Q（a，b′），给出如下定义：
若b′=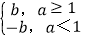
，则称点Q为点P的限变点．例如：点（2，3）的限变点的坐标是（2，3），点（-2，5）的限变点的坐标是（-2，-5）．
（1）①点(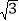
，1)的限变点的坐标是 ；
②在点A（-2，-1），B（-1，2）中有一个点是函数y＝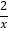
图象上某一个点的限变点，这个点是 ；（填“A”或“B”）
（2）若点P在函数y=-x+3（-2≤x≤k，k＞-2）的图象上，其限变点Q的纵坐标b′的取值范围是-5≤b′≤2，求k的取值范围 ；
（3）若点P在关于x的二次函数y=x2-2tx+t2+t的图象上，其限变点Q的纵坐标b′的取值范围是b′≥m或b′＜n，其中m＞n．令s=m-n，求s关于t的函数解析式及s的取值范围 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校实施课程改革，为初三学生设置了A，B，C，D，E，F共六门不同的拓展性课程，现随机抽取若干学生进行了“我最想选的一门课”调查，并将调查结果绘制成如图统计图表（不完整）
选修课
A
B
C
D
E
F
人数
20
30
根据图标提供的信息，下列结论错误的是（ ）
A. 这次被调查的学生人数为200人 B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中最想选F的人数为35人 D. 被调查的学生中最想选D的有55人
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两班举行班际电脑汉字输入比赛，各选10名选手参赛，各班参赛学生每分钟输入汉字个数统计如下表：
通过计算可知两组数据的方差分别为S2甲=2.0，S2乙=2.7，则下列说法：①两组数据的平均数相同；②甲组学生比乙组学生的成绩稳定；③两组学生成绩的中位数相同；④两组学生成绩的众数相同.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市少体校为了从甲、乙两名运动员中选出一名运动员参加省运动会百米比赛，组织了选拔测试，分别对两人进行了五次测试，成绩（单位：秒）以及平均数、方差如表：
甲
13
13
14
16
18
x
=14.8S
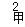=3.76乙
14
14
15
15
16
x
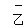=14.8S
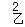=0.56学校决定派乙运动员参加比赛，理由是 ．
相关试题
