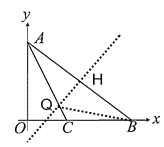
【题目】如图,在![]() 中,
中,![]() 是原点,
是原点,![]() (0,3),
(0,3),![]() (4,0),
(4,0),![]() 是
是![]() 的角平分线.
的角平分线.

(1)确定![]() 所在直线的函数表达式;
所在直线的函数表达式;
(2)在线段![]() 上是否有一点
上是否有一点![]() ,使点
,使点![]() 到
到![]() 轴和
轴和![]() 轴的距离相等,若存在,求出点
轴的距离相等,若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)在线段![]() 上是否有一点
上是否有一点![]() ,使
,使![]() 是等腰三角形,若存在,直接写出 点
是等腰三角形,若存在,直接写出 点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)直线AB的解析式为:![]() ;(2)点
;(2)点![]() 的坐标为(1,1);(3)点Q的坐标为:(
的坐标为(1,1);(3)点Q的坐标为:(![]() ,
,![]() ).
).
【解析】
(1)直接利用待定系数法求解即可;
(2)过点C作CE⊥AB,设OC=CE=x,则BC=4-x,求出BE=2,然后在Rt△BCE中,利用勾股定理构建方程求出OC得到C点坐标,求出直线AC的解析式,联立直线AC的解析式和y=x,求出交点坐标即可;
(3)作线段AB的垂直平分线QH交AC于Q,交AB与H,设出直线QH的解析式,求出点H的坐标,代入可得直线QH的解析式,联立直线QH与直线AC的解析式,求出交点坐标即可.
解:(1)设直线AB的解析式为:y=kx+b,
代入A(0,3),B(4,0)得:![]() ,
,
解得: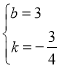 ,
,
∴直线AB的解析式为:![]() ;
;
(2)过点C作CE⊥AB,
∵AC平分∠OAB,
∴OC=CE,
∴设OC=CE=x,则BC=4-x,
易证△AOC≌△ACE,则AE=OA=3,
∵AB![]() ,
,
∴BE=5-3=2,
在Rt△BCE中,CE2+BE2=BC2,即x2+22=(4-x)2,
解得:![]() ,
,
∴C(![]() ,0),
,0),
设直线AC的解析式为:y=mx+n,
代入A(0,3),C(![]() ,0)得:
,0)得: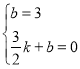 ,
,
解得:![]() ,
,
∴直线AC的解析式为:y=-2x+3,
∵点![]() 在线段
在线段![]() 上,且到
上,且到![]() 轴和
轴和![]() 轴的距离相等,
轴的距离相等,
∴点P在直线y=x上,
联立![]() ,解得:
,解得:![]() ,
,
∴点![]() 的坐标为(1,1);
的坐标为(1,1);
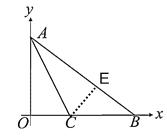
(3)∵点Q在线段AC上,△AQB是等腰三角形,
∴如果存在,只有AQ=BQ一种情况,
作线段AB的垂直平分线QH交AC于Q,交AB与H,
∵直线AB的解析式为:![]() ,
,
∴ 设直线QH的解析式为:![]() ,
,
∵A(0,3),B(4,0),
∴H(2,![]() ),
),
将点H(2,![]() )代入
)代入![]() 得:
得:![]() ,
,
解得:![]() ,
,
∴直线QH的解析式为:![]() ,
,
联立直线QH与直线AC解析式得: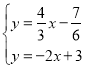 ,
,
解得:![]() ,
,
∴点Q的坐标为:(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 的垂直平分线交
的垂直平分线交 于点
于点 ,交
,交 于点
于点 .
. 
(1)若
 ,求
,求 的长;
的长;(2)若
 ,求证:
,求证: 是等腰三角形.
是等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某旅行团去景点游览,共有成人和儿童20人,且旅行团中儿童人数多于成人.景点规定:成人票40元/张,儿童票20元/张.
(1)若20人买门票共花费560元,求成人和儿童各多少人?
(2)景区推出“庆元旦”优惠方案,具体方案为:
方案一:购买一张成人票免一张儿童票费用;
方案二:成人票和儿童票都打八折优惠;
设:旅行团中有成人a人,旅行团的门票总费用为W元.
①方案一:
 _____________________;
_____________________;方案二:
 ____________________;
____________________;②试随着a的变化,哪种方案更优惠?
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
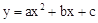 (a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:x
﹣3
﹣2
﹣1
0
1
2
3
4
5
y
12
5
0
﹣3
﹣4
﹣3
0
5
12
给出了结论:
(1)二次函数
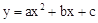 有最小值,最小值为﹣3;
有最小值,最小值为﹣3;(2)当
 时,y<0;
时,y<0;(3)二次函数
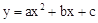 的图象与x轴有两个交点,且它们分别在y轴两侧.
的图象与x轴有两个交点,且它们分别在y轴两侧.则其中正确结论的个数是
A. 3 B. 2 C. 1 D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】2002年国际数学家大会在北京召开,大会选用了赵爽弦图作为会标的中心图案.如图,由四个全等的直角三角形与一个小正方形拼成一个大正方形.如果大正方形的面积是25,直角三角形较长的直角边长是a,较短的直角边长是b,且(a+b)2的值为49,那么小正方形的面积是( )

A.2B.0.5C.13D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 在平面直角坐标系中的位置如图所示,则下列结论:
在平面直角坐标系中的位置如图所示,则下列结论:①
 ;②
;② ;③
;③ ;④
;④ .
.其中,正确的结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程_____.

相关试题

